こんにちは。Horyです。
前回の記事では円運動について、等速円運動と非等速円運動の問題について解説しました。
今回の問題解説は少し変わり種の問題で、円運動とジェットコースターの設計を絡めた問題になります。
今回も頑張りましょう。
ジェットコースターの設計

今回の問題はどうやったら安全なジェットコースターを作れるかがテーマになります。
以下に軌道の図を示します。
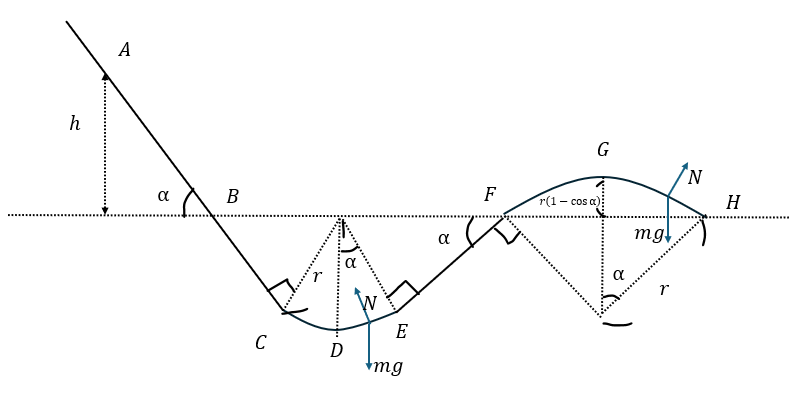
- A→C・・・斜面落下運動
- C→E・・・円運動
- E→F・・・斜面上昇運動
- F→H・・・円運動
(1)解答・解説
まずは、上に示したレールの各部分における垂直抗力を求めてみます。
斜面運動についてはレールについて垂直な方向の力の釣り合いを書いて、円運動については極座標で動径方向の運動方程式を記述します。
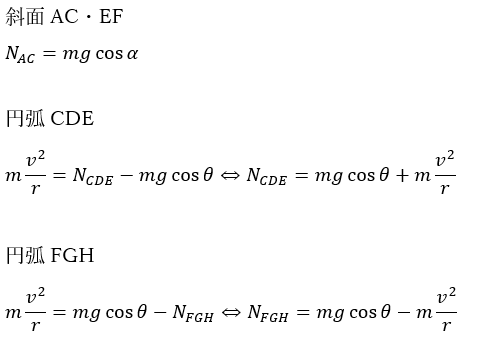
ちょっとグラフに記述してみます。
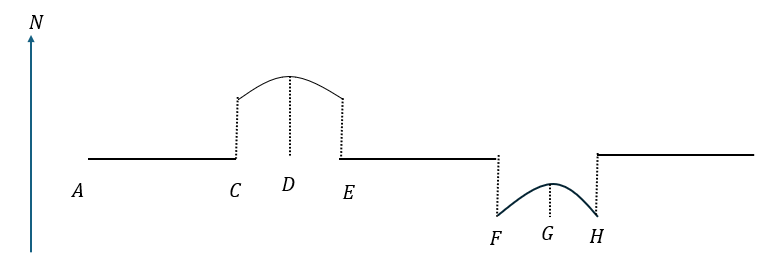
このグラフを見ると斜面上では抗力が一定となります。
一方で、円運動になった瞬間に抗力は急激に変化します。
抗力の最大値は点D,最小値は点F,Hになります。
点Dと点F,Hでの抗力を試しに求めてみます。
解き方は以下の手順に従って解きます。
- 位置エネルギーの基準点を決める(今回点Dを基準)
- エネルギー保存則で速度の二乗を求める
- 速度を中心方向に代入して求める
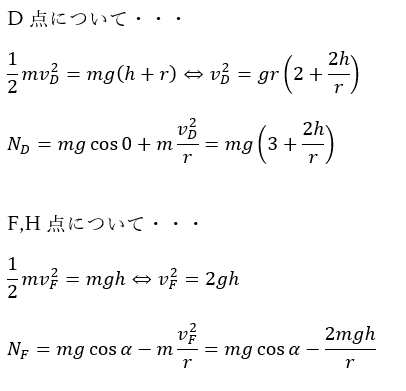
(2)解答・解説
これは、角度を変えずに高さを変えたら、どのぐらいの高さで安全に運行できるかという問題です。
F点で浮き上がらずに脱線しないようにするにはF点で垂直抗力が0以上でないといけません。
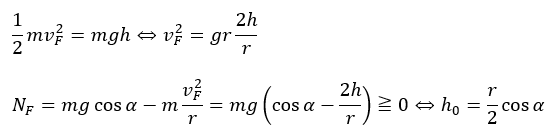
よって、角度を変えないのであれば、高さが上のh0より小さくなるように設定すれば事故が起きないようにできます。
(3)解答・解説
次の問題は角度についてデス。ジェットコースターが安全に運行できる高さについて、以下の不等式で挟めます。
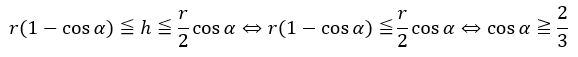
つまり、角度を48.2°より小さくすれば安全というわけです。



コメント