こんにちは。Horyです。
皆さんは「円周率が3.05よりも大きいこと」を証明する問題を知っていますでしょうか?
非常に有名な問題なのでこの記事で解説する必要もないと思います。
今回の記事ではこの問題の攻略について解説すると共に、「円周率とは何なのか?」ということや本問題の小話を解説しようと思います。
今回も頑張りましょう。
円周率とは何か?
本問を解説する前に円周率とはそもそも何なのでしょうか?
学生に「円周率を説明してみて」と質問すると口を揃えて「3.14」と答えます。
答えが間違っていると言い切ることは出来ませんが、本質が分かっているのかと考えるとちょっと疑問が残ります。
「円周率とは何か?」という質問の本質は小学校5年生の時に行った算数の授業に隠されています。
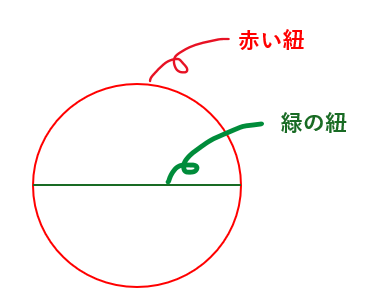
小学5年生の時に上の図の赤い紐と緑の紐で長さ比べをしたことを覚えていますでしょうか?
- 赤い紐の長さ・・・円周
- 緑の紐の長さ・・・円の直径
円の大きさを変えても赤い紐と緑の紐の長さの比が一定で「赤い紐:緑の紐=1:3.14・・・」になったと思います。
そして、「3.14・・・」と無理数で表される数をπという文字で置き換えようと言うのが実験の結論だったかと思います。
まとめると、「円の大きさがどのようになっても直径:円周 = 1:π」ということを表しています。
そして、円の半径をrと文字で置くと・・・

面積で比較する方法
円周率が3.05よりも大きいことを面積比較で証明します。
手っ取り早い方法は正多角形を円に内接する方法です。
「円は正n角形のnを無限大にした図形」です。
(周の長さで比較したい気持ちも分かりますが、余弦定理を使うことでルートの数が多くなって収拾が付かなくなります)
円に内接しているので「正多角形の面積 < 円の面積」になります。
私たちが長さを求めることができる最もnが大きい正多角形は正24角形です(45°-30°=15°)。
今回は半径1の円に内接する正24角形を考えます。
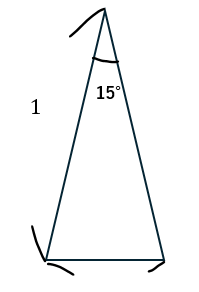
上の図に示す三角形の面積を24倍します(この三角形は円に内接していません。だから、正弦定理を使うのは難しそうです)。
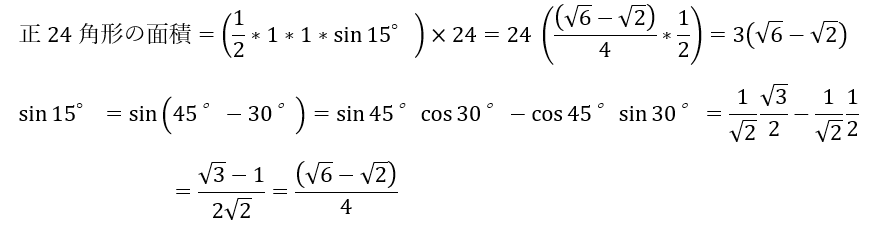
後は円と正多角形の面積を比べるだけです。

以上のことから3(√6-√2)が3.05よりも大きいことを示せれば勝ちです。
ここで、ちょっとした裏技です。
√が2つあって非常に厄介なので二乗してルートの数を1つに減らします。

以上の事から・・・

余談
この問題に関する余談です。
この問題が出題された当時、文部科学省はゆとり教育という方法を取り入れていて、その中で「円周率を3にしよう」という議論が上っていました。
本問題は「円周率を3にすること」に対する問題提起であると共に、「計算や原理・定義と真摯に向き合い横着をしないように」という作問者からのメッセージなのではないかと思います



コメント