こんにちは。Horyです。
前回の記事では共分散と相関係数の意味や定義に関して解説しました。
今回の記事では共分散と相関係数に関する有用な定理を解説します。
共通テストで出ることはないですが、覚えといた方が良いと思うので頑張りましょう。
式に関して証明する前に登場する文字の定義を簡単に解説します。
データに関してはx,yに関するデータがそれぞれn個あるとします。

これらの前提条件を利用して定理を解説しようと思います。
相関係数と軸の入れ替え
横軸と縦軸を入れ替えた場合に相関係数がどうなるかを考えてみます。
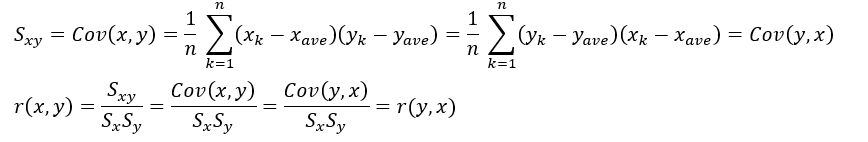
以上の事から、縦軸と横軸を入れ替えても共分散が変化しないので相関係数も変化しません。
共分散と定数の和
共分散について、データの中身に細工をします。
Covの中身がx,yでしたが、これに定数が加算されていたらどうでしょうか?
試しに定数をA,Bと置いて、x,yに足してみましょう。
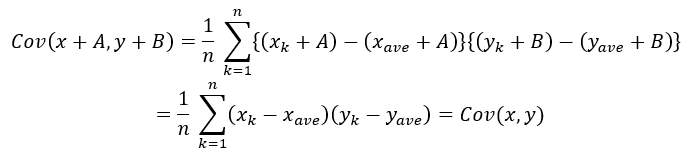
以上のことから定数を加算したとしても共分散自体は変化しません。
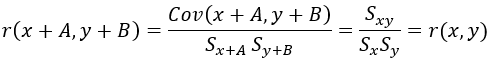
相関係数も変化しません。
共分散と定数の積
共分散に関して、データの中身に細工を行います。
Covの中身がx,yでしたが、これに定数が掛け算されていたらどうなるでしょうか?
試しに定数をA,Bと置いてx,yに掛けてみましょう。
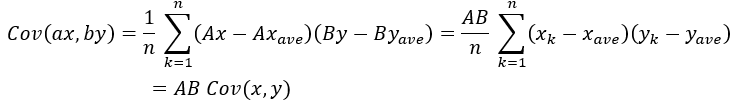
定数を掛け算したときは共分散も変化します。
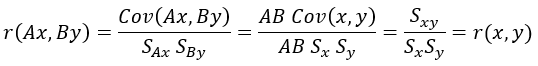
積に関して、共分散は変化するにも関わらず相関係数は変化しません。不思議ですねぇ。
相関係数の範囲
前回の記事で相関係数の範囲に関して話しましたが証明はしていなかったので証明します。
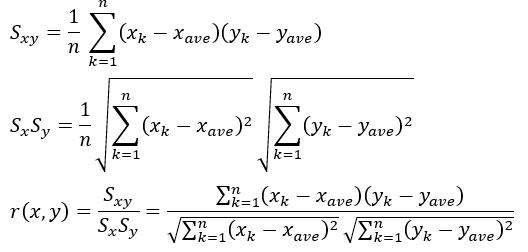
ルートがうざったいのでとりあえず二乗します。
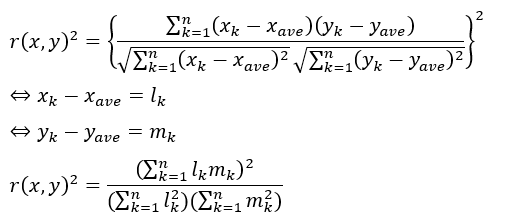
分母と分子の形ってどこかで見覚えがありますねぇ・・・
コーシーシュワルツの不等式が利用できそうです。
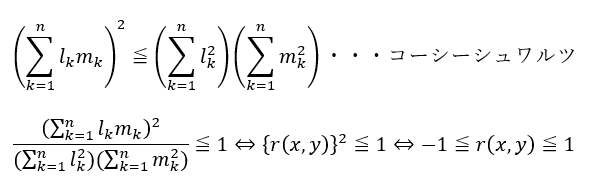
以上により相関係数の範囲が証明されました。


コメント