こんにちは。Horyです。
前回の記事では化学結合に関する基礎的な事項をまとめると共に、金属の性質に関して原理から解説しました。
今回の記事では、単位格子に関して簡単に解説すると共に、高校化学で出てくる単位格子をまとめようと思います。
今回も頑張りましょう。
単位格子について・・・
単位格子とは結晶中の原子の空間構造を表したモノの最小単位です。
原子配列が空間的に繰り返しパターンを持つモノで、単位格子を集めると結晶になります。
以下に単位格子の一例を示します。
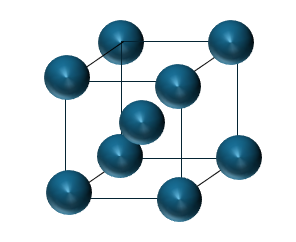
上に示すような単位格子が何個も集まって結晶ができています。
そもそもどうやって調べたのかというと、結晶にX線を透過して調べています(X線が透過しなかった部分に原子がある)。
結晶格子を書くときは粒子の中心を書けば良いです。
そして、一番大事な点で、こんなモノが何で導入されたかについてですが、金属の密度から原子の半径を求めたかったがために導入されました。
単位格子と計算
単位格子と計算について考えます。
計算に必要なパラメータ(文字)を以下のように設定します。
- 密度・・・d [g/cm3]
- 単位格子の体積・・・V[cm3]
- 単位格子の質量・・・m [g]
- 単位格子をn個集めると結晶になる
- 結晶の質量M [g]
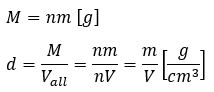
仮に単位格子が立方格子(立方体)だとして一辺の長さをx [cm]とすると・・・
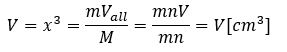
ここで単位格子中にk個の原子が存在するとして、この原子のモル質量をP[g/mol]とします。また、アボガドロ数をNaとします。
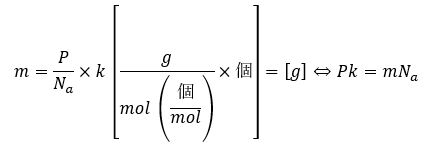
- 上の式の意味
- 左辺・・・k個の原子をモル質量だけ集めた質量
- 右辺・・・単位格子をアボガドロ数集めた質量
上の2つの式を合わせると・・・
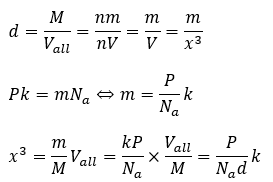
基本的に、入試では密度を導出することが多いです。理科は導出する値と同様に単位も重要です。基本的に理科では数値と単位は同じ価値であるべきです。
以下の記事でも書きましたが、理科の計算で単位検算も行うとミスは飛躍的に減ります。
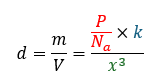
- 赤い部分・・・粒子1つの質量
- 青い部分・・・単位格子中の粒子数
- 緑の部分・・・単位格子の体積
また、単位格子の問題で、長さがnm (ナノメートル)で表記されていることが多いです。
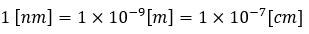
瞬時に単位変換ができるようになってほしいです。
金属結晶の単位格子
高校化学で習得する必要がある単位格子は基本的に立方格子(立方体の格子)です。
そして、金属結晶で出てくる代表的なものは3つあります。
- ①;体心立方格子 (bcc)
- ②;面心立方格子 (fcc)
- ③;六方最密構造 (hcp)
これらについて個別に解説します。また、1つの原子に対して最近接に存在する原子を配位子と言って、配位子の数を配位数といいます。
体心立方格子
まずは、体心立方格子についてです。以下に図を示します。
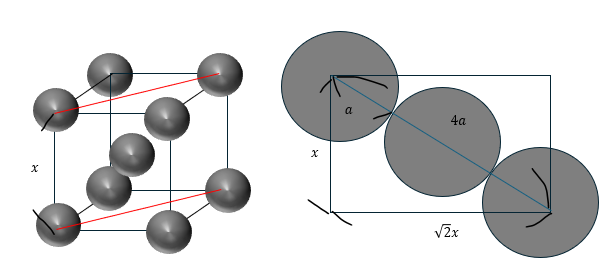
上に示すように立方体の頂点と中心に原子があります。そのため、単位格子中の原子数は2個です。また、配位数は8個になります。
単位格子の一辺の長さをxとして、原子の半径をaとします。三平方の定理で原子の半径aはxで表せます。
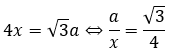
ここで、充填率と密度を求めます。充填率は、単位格子中に粒子がどのくらいの割合を占めているかを%で出したモノです。
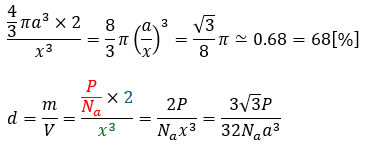
以上により、充填率と密度を求めました。
面心立方格子
次に面心立方格子についてです。以下に図を示します。
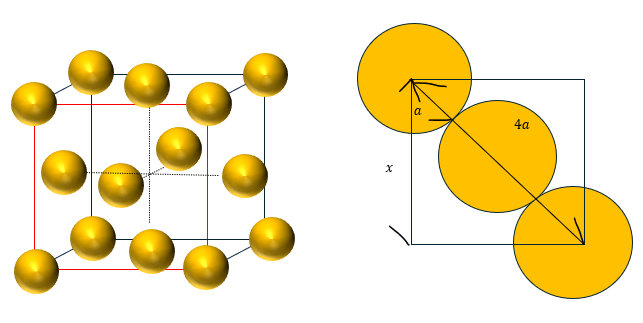
この格子は立方格子の各頂点と面の中心に原子の中心があります。そのため、単位格子中に原子は4つ存在し、配位数は12個です(単位格子を2つ並べる)
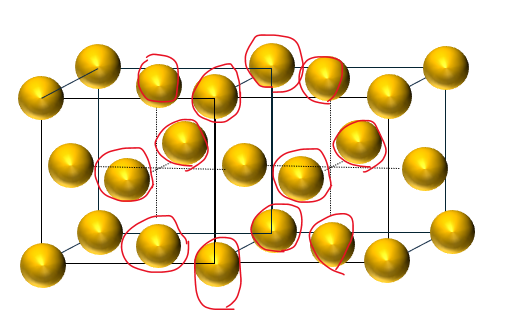
こちらも先ほどと同様の手法で充填率と密度を求めてみます。
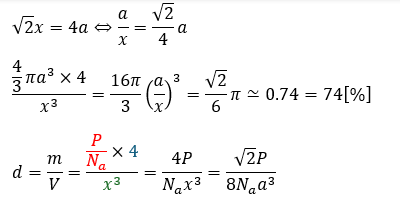
六方最密構造
最後に六方最密構造についてです。以下に図を示します。
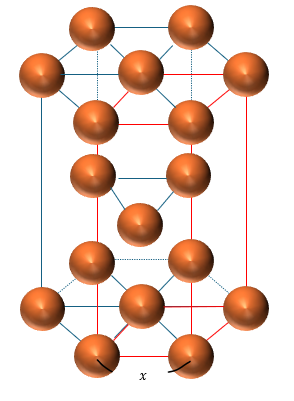
まぁ、これが多くの受験生の悩みの種だと思います。上の図の赤い部分はこの立体の体積の1/3になり、原子が2個入ってます。
ここで、充填率を求めたいですが、高さhをどうにかしたいですね。
ここで、知ってると得する知識ですが、この単位格子を上から見たとき、2段目の原子は三角形の重心になります。
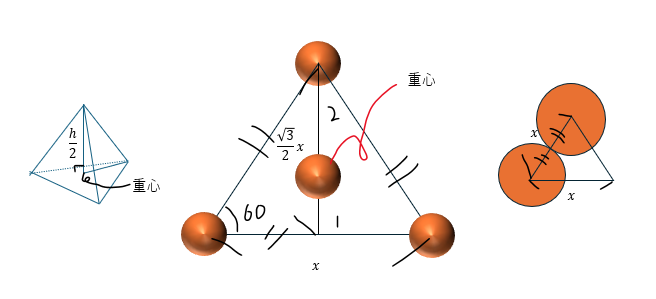
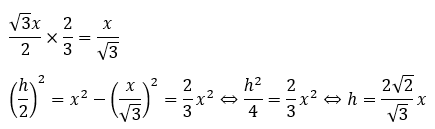
高さが求められたので、充填率と密度を求めてみます。赤い部分の体積と原子の個数で求めます。
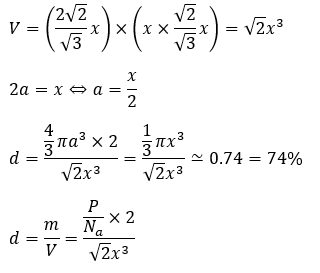
六方最密構造と面心立方格子の充填率はほぼ同じになります。また、配位子の数も12個です。



コメント