こんにちは。Horyです。
前回の記事では交流回路について解説するとともに、
交流電源に抵抗・コンデンサ・コイル・RLC並列回路などの様々な素子を接続させたときの電流の振る舞いなどについて微分方程式をといて説明しました。
今回の記事では交流におけるRLC直列回路について、回路の方程式から微分保定式を解いて電流などの振る舞いを解説しようと思います。
今回も頑張りましょう。
RLC交流直列回路
RLC直列回路について以下に示す回路を考えます。
ただし、抵抗の抵抗値をR, コンデンサの電気容量をC, コイルの自己インダクタンスをLとします。
このとき、電源の電圧・コンデンサにたまる電荷・回路に流れる電流の振る舞いを考えます。
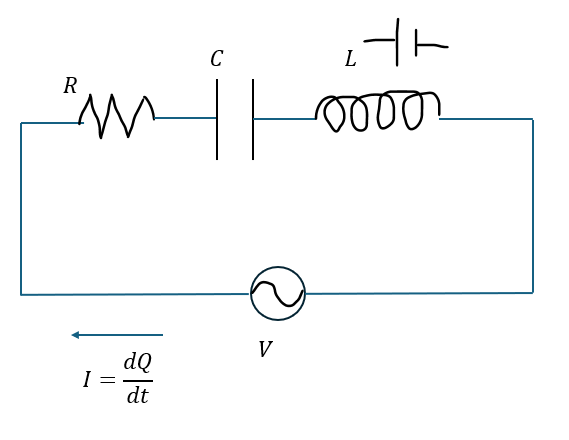
ただし、電圧・電流・電荷の式は以下のように書けるとします。
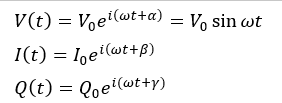
回路の方程式を立てます。「電位降下の和が起電力」になります。
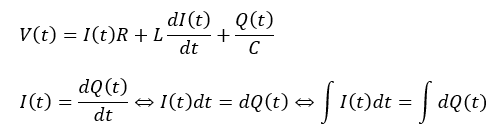
この微分方程式は空気抵抗ありの単振動微分方程式をさらに複雑にしたものです。
正直、これだけから解を見つけるのは困難なので、先に電圧・電流・電荷の式が上の形で書けることを示しました。
問題を解いていきます。
微分方程式を解く
微分方程式を解きます。

かなり長い式になりましたが、電流の振る舞いが分かりました(赤い部分)。
正直、ここに至るまでに、単振動型微分方程式(複雑)・三角関数の合成・オイラーの公式など高級な定理ばかり使ってきましたが、入試ではこんなのは出されないので安心してください(出たとしても誘導あり)。
赤い式を回路の方程式へ代入します。
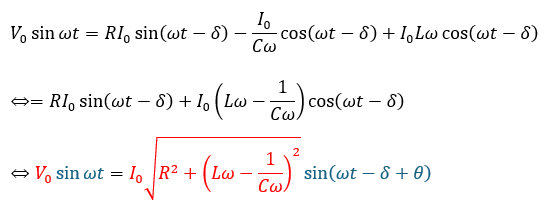
赤い部分と青い部分の角度が一致していないとおかしいです。
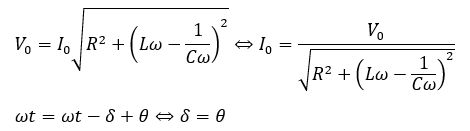
よって、電圧と電流の式を直してみると・・・
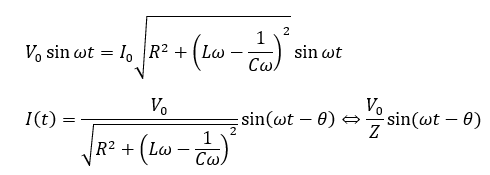
電圧降下を求めろ
抵抗・コンデンサ・コイルによる電圧降下を求めてみます。
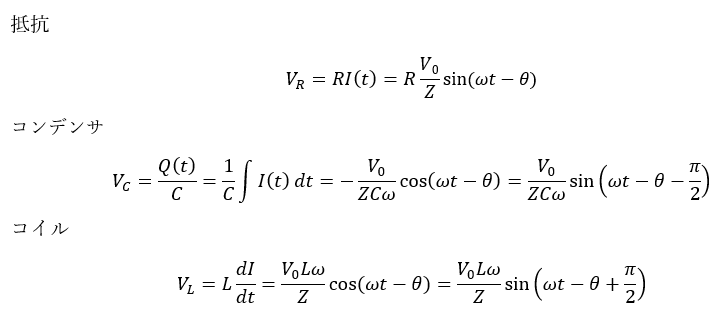


コメント