こんにちは。Horyです。
私たちはこれまでに電気回路の問題について取り組んできましたが、これまでに取り組んできた問題は全て直流回路でした。
直流回路は電圧や電流の流れが1つの方向しかとらない回路です。
直流回路がある一方で、交流回路というものがあります。交流回路は電圧・電流の流れが周期的に変わる回路のことを言います。
今回の記事では交流回路の基礎事項を解説すると共に、交流におけるRLC並列回路の問題を解いていこうと思います。
今回も頑張りましょう。
交流回路の基礎事項
交流回路とは電圧・電流の方向が周期的に変わる回路です。
具体的には、起電力の式が以下に示すような時刻の三角関数で表される回路のことです。

電圧・電流の振幅をルート2で割った値を実効値と言います。これは、そういうものだと覚えてください。
また、交流電源は記号で以下のように書きます。
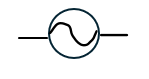
問題で上の図のような記号が出たら交流回路の問題です。
また、交流回路では、電圧の式について、電流の式が遅れていたり、進んでいたりします。
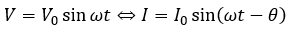
電圧の式の角度ωtの部分を位相と言って、θを見ることで電流が電圧の位相と比較してどの程度遅れているか進んでいるかを議論します。
また、直流回路では、電圧を流れる電流量で割った値を抵抗と言いますが、交流回路では抵抗と呼ぶのではなくリアクタンスと呼びます。
リアクタンスは最大電圧を最大電流で割った量です。
ここで、学習したことをまとめてみます。
- 直流回路・・・電圧や電流の向きが変化しない
- 抵抗は電圧を電流で割った量
- 交流回路・・・電圧や電流の向きが周期的に変化
- 抵抗は最大電圧を最大電流で割った量でリアクタンス
- 実効値は最大電圧・電流をルート2で割った量
RLC並列交流回路
以下に示すのはRLC並列交流回路に関する問題です。

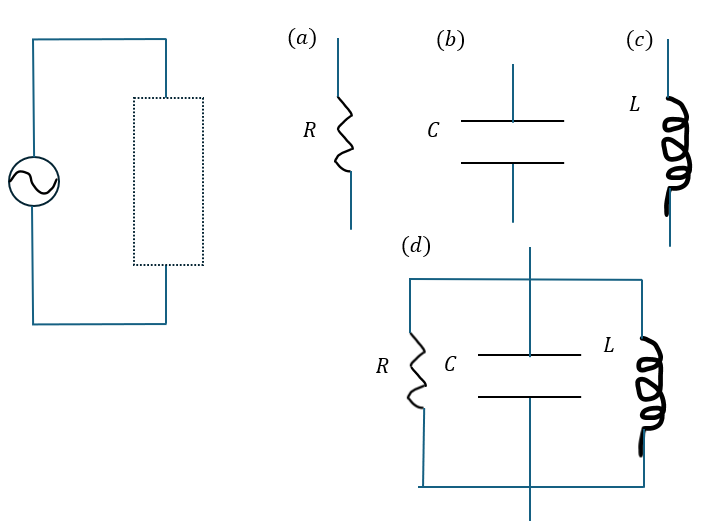
この問題を例に解説します。
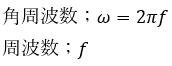
(a)抵抗素子の接続
抵抗素子を接続した場合を考えてみましょう。これは簡単です。
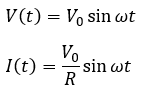
消費電力とその時間平均を求めてみます。
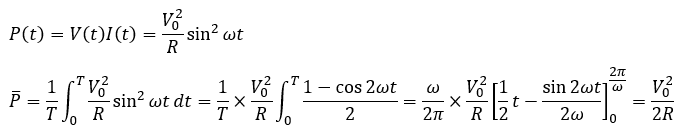
消費電力の時間平均を求めました。
(b)コンデンサ素子の接続
コンデンサを接続した場合を考えてみましょう。
回路の方程式を解いて微分方程式を解きます。
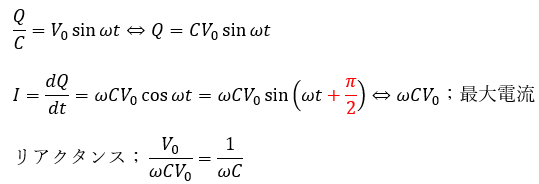
ここで、コンデンサの静電エネルギーを求めていきます。
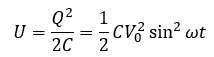
また、この回路の消費電力の時間平均を求めると・・・
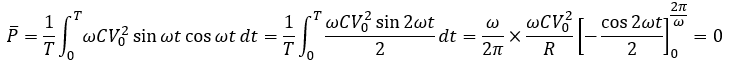
この回路の消費電力の時間平均は0になります。つまり、コンデンサはエネルギーを消費しません。
(c)コイル素子の場合
コイルを接続した場合を考えましょう。誘導起電力を考えます。
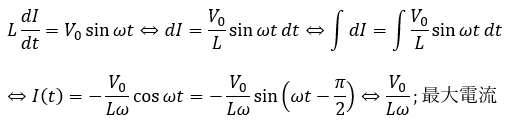
この微分方程式について、積分定数は書きません(交流回路では積分定数は考えません)。
これが解です。

コンデンサの場合と同様に消費電力の時間平均は0になります。だから、コイルはエネルギーを消費しません。
(d)RLC並列回路の場合
RLC並列交流回路を考えます。今回のメインテーマになります。
これまでに取り組んだ(a)~(c)の全てを利用します。
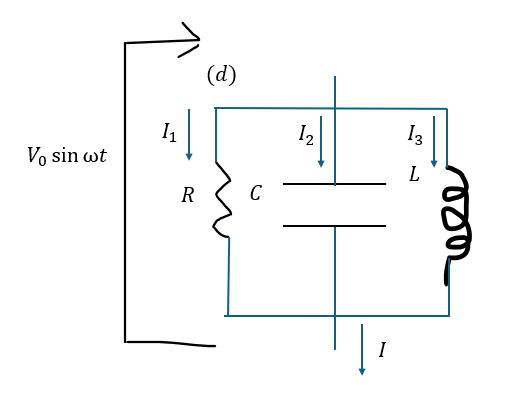
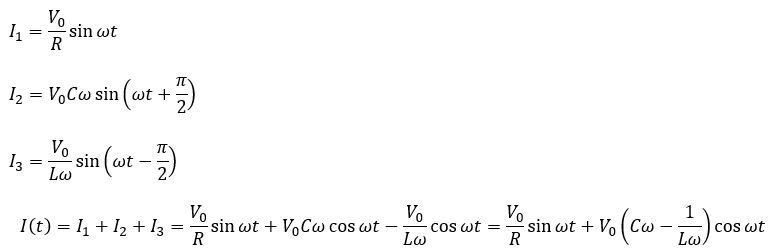
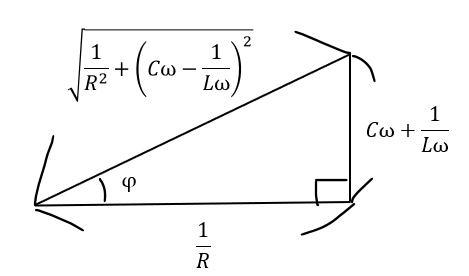
これについて、三角関数の合成を使います。
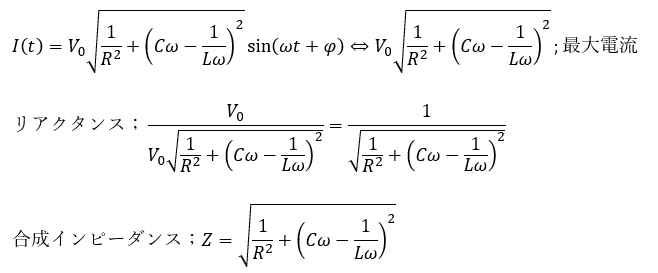
交流RLC回路について、リアクタンスに抵抗を考慮した数値をインピーダンスといいます。
三角関数の合成に関してはこちらの記事で復習してみてください。



コメント