こんにちは。Horyです。
今回の記事では二次不等式が関係する整数問題に関して解説します。
二次不等式に関してはこちらの記事で基本は説明したので読んでおいてください。
今回も頑張りましょう。
問題
以下に示すのはこの記事で解説する問題です。

この問題を例に解説します。
問題を解く前の下準備
問題を解く前の下準備です。
まず、この二次関数は下に凸の二次関数です。
そして、不等式を満たす整数解が1つという情報から二次方程式の2解の差がどうなるか?ということを瞬時に思いつけないとしんどいです。
また、何気に忘れやすいことですが、そもそも、判別式>0でないと満たす整数が存在しないことになるので、まずは判別式です。
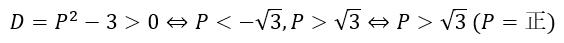
ひとまず、二次方程式と見て解の公式で解を導出してみます。
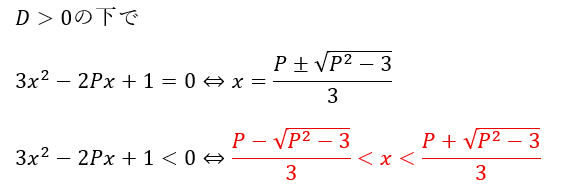
赤い不等式の中に整数がちょうど1つ存在すればいいです。
解答・解説
下準備も終わったので解答・解説です。
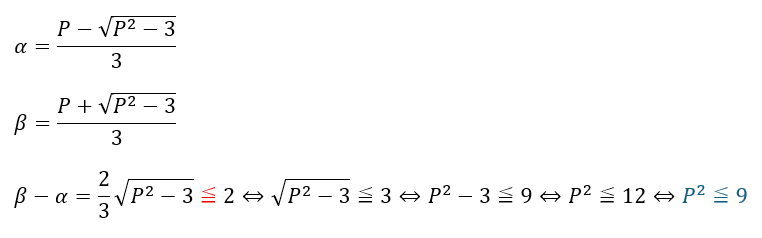
- 赤い部分;あくまで2以下という点が注意です
- 青い部分;Pが正の整数ということを考えれば・・・
そのため・・・
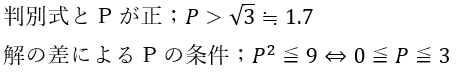
上の二つの不等式の共通部分にあるPは「P=2,3」しか存在しません。
だからP=2,3が解だ!「やったぜ!」で解答を終わってしまう人は実に残念でもったいないです。
前回の記事で説明した十分性の確認を怠っています。
不十分な理由は2解の差に関する不等式です。何でかは自分で考えてみてほしいです。
なので、実際に代入して解を求めてみます。
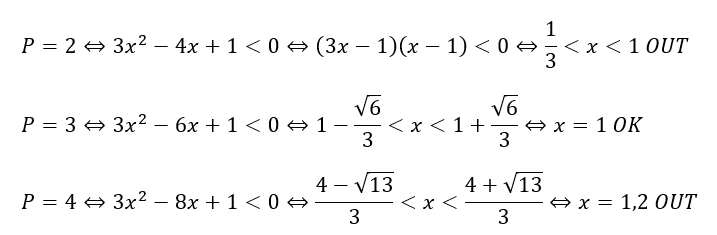
以上から、満たすPは「P=3」のみです。



コメント