こんにちは。horyです。
二変数関数の最大・最小値を求める問題については予選・決勝法を用いる問題や角度θを用いて一変数化を持ち手解く問題を今までに紹介しました。
今回は二次方程式の解と係数の関係を用いて最大値・最小値を求める問題を紹介します。
今回も頑張りましょう。
問題 二変数関数の最大・最小
以下は今回の記事で取り組む問題です。
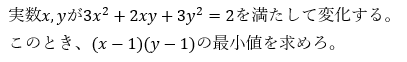
この問題を例に解説します。
問題を解く前の下準備
問題を解く前の下準備です。
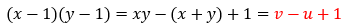
上の式を展開すると式の中に二次方程式の解と係数の関係を見いだせます。
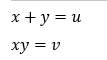
xとyは以下の二次方程式の実数解と見ることができます。
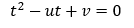
またxとyの条件をuとvの条件に置き換えれます。
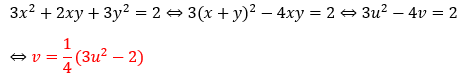
uとvは上の二次関数上を動きます。
問題 解答・解説
問題の解答・解説です。
まず、二次方程式の実数解条件より判別式Dが0以上です。
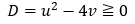
次にuの範囲を導いてあげます。
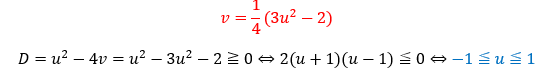
次に、最小値を求める関数をuのみで表します。
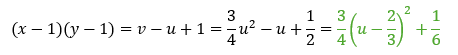
上の緑の式は下に凸の二次関数となります。
最小値は・・・
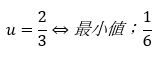



コメント