こんにちは。horyです。
今回も三角関数の最大値・最小値に関する記事になります。
その中で、今回は倍角の公式・半角の公式を用いるものについて簡単にまとめました。
以下の記事を読んでいない場合、この記事を読む前に読んでおくことをお勧めします。
三角関数の最大値・最小値
以下はこの記事で取り組む問題です。

この問題を例に解説します。
問題を解く手順
問題を解く手順を(1)・(2)ともに箇条書きでまとめます。
(1)の手順
- 倍角の公式・半角の公式で「2次→1次」へ
- 三角関数の合成でsinに統一
(2)の手順
- 和「sinθ+cosθ=t」とおく
- 積「sinθcosθ」をtの式で表す
- 関数をtの式で統一
以下はsin・cosのどちらかに統一するときの統一方法です。
- 倍角・半角の利用→三角関数の合成
- 倍角・半角の利用→sinかcosのn次式→グラフ
- sinθ+cosθ=t→関数をtの式に統一→グラフ
もちろん。sinかcosの統一に単位円の公式を用いることもよくあります。
単位円の公式は以下の通りです。
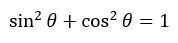
(1)解答・解説
まず、倍角の公式・半角の公式を用いて「2次→1次」にします。
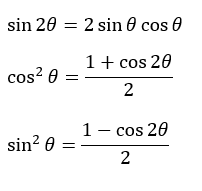
上の公式を利用します。
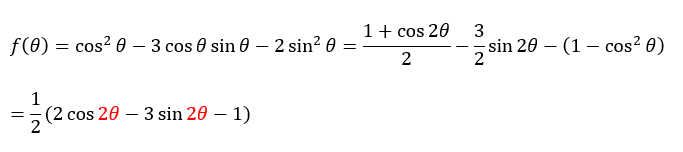
角度の変数が一致しているので合成を用いて統一できます。
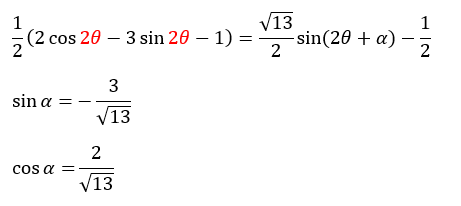
角度の範囲は以下の通りです。
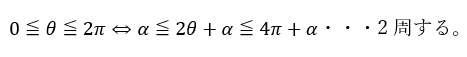
以上より最大値・最小値は・・・

今回の問題は最大値・最小値を求めるだけの問題なので、最大値・最小値の時のθをわざわざ求める必要はないです。
(2)解答・解説
重要問題の内の1つです。
まず、和「sinθ+cosθ=t」とおきます。
tは自分で設定した文字なので範囲に関する説明が必要です。
ここで、tは三角関数の合成で統一することができます。
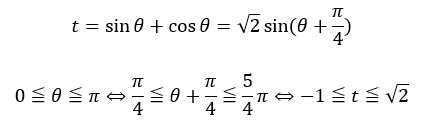
以上により、tに関する説明は完了です。問題はどのようにtに統一するかです。
積「sinθcosθ」をtで表せれば突破できそうです。
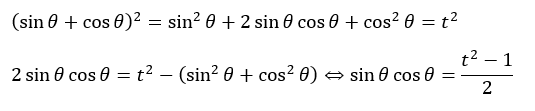
以上により、関数をtのみで表せそうです。
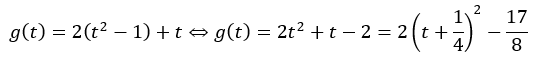
tの二次関数にすることができました。
後は、グラフの性質を用いて解くだけです。
以下は二次関数の情報になります。

以上より、最大値・最小値は・・・
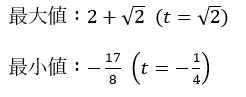



コメント