こんにちは。Horyです。
今回の記事では三角形の重なった部分の面積を求める問題を解説しようと思います。
こういった問題は共通テストでも頻出しますので知っておいて損はないと思います。
今回も頑張りましょう。
三角形の重なり
以下に示すのはこの記事で取り組む問題になります。

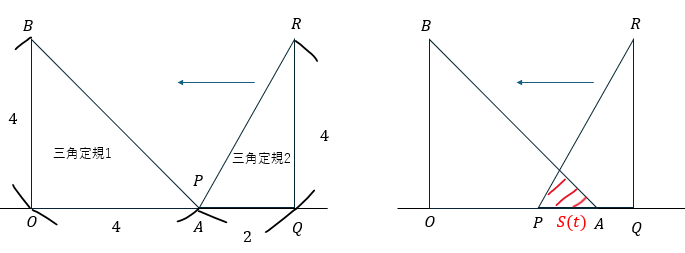
この問題を例に面積を時刻の関数で表してみます。
問題を解く前の下準備 (図形の形に注目する)
問題を解く前の下準備です。
図形の形に注目してほしいです。
図に示してあるのは重なった部分が三角形の時ですが、三角形の時ばかりではありません。
つまり、時刻によって重なった部分の形が変わるので面積の求め方が違います。
場合分けをする必要がありますね。
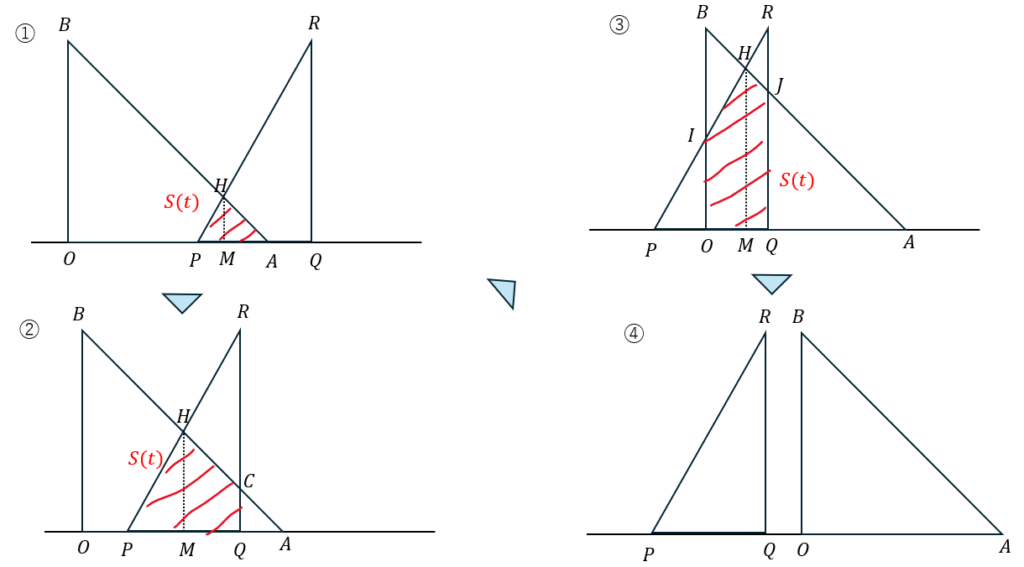
三角形の面積を求めるには底辺と高さの情報が必要です。
そのため、三角定規の交点と交点から水平面に下ろした垂線の足を記号で決めます。
- 状態 ①;2つの三角形に分ける
- 状態 ②;三角形と台形に分ける
- 状態 ③;2つの台形に分ける
- 状態 ④;重なっている部分はない
このように場合分けが出来ます。
それぞれで面積を求めていきましょう。
状態 ① (2つの三角形)
重なった部分が2つの三角形に分けられるときの面積を求めてみましょう。
- 状態の始まり;PがAに接触したとき (t=0)
- 状態の終わり;QがAに接触したとき (t=2)
三角形は水平面に平行に移動するので相似条件が使えそうです。
- △OAB ∽ △MAH ⇔ HM=AM
- △PQR ∽ △PMH ⇔ HM=2PM
- AM:PM=2:1
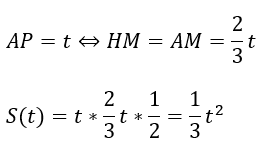
状態 ② (三角形と台形)
重なった部分が三角形と台形に分けられるときの面積を求めてみましょう。
台形と書いていますが台形の面積は求めないでください(面倒くさいから)。
こういうのは引き算で考えます。
- 重なり;△PHA-△QAC
- 状態の始まり;QがAに接触したとき (t=2)
- 状態の終わり;PがOに接触したとき (t=4)
相似条件は状態①と同様に使えます。
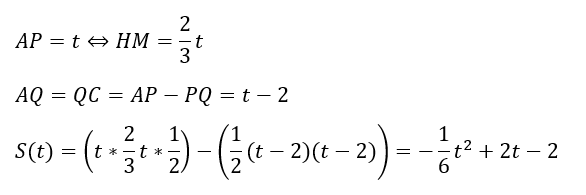
状態 ③ (2つの台形)
これも台形と書いていますが台形の面積は求めないでください。
- 重なり;△APH-△POI-△AQJ
三角形の面積は先ほどと同様に求めていきます。
- 状態の始まり;PがOに接触したとき (t=4)
- 状態の終わり;QがOに接触したとき (t=6)
状態②と同様の方法で求めていきます (相似条件をつかう)
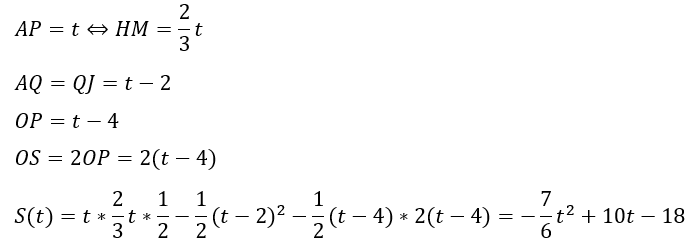
状態 ④ (重なり合う部分がない)
- 状態の始まり;QがOに接触したとき (t=6)
当たり前ですが重なり合う部分がないので0です。
グラフ化
状態①~④をグラフ化してみます。
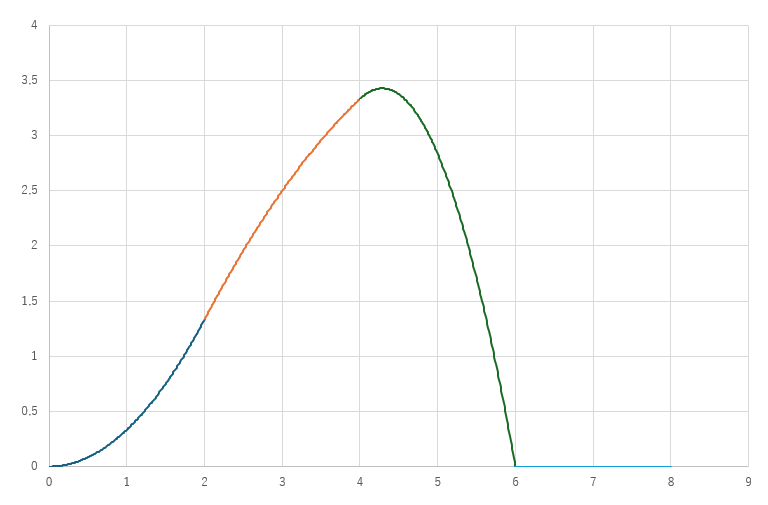
二次関数や図形の性質といった様々な知識を用いる非常に良い問題でした。



コメント