こんにちは。Horyです。
今回の記事では三角形の二等分に関する問題に取り組みます。
今回の記事で言いたいことは煩雑な計算であっても工夫をすることで比較的に簡単に解くことが出来ると言うことです。 今回も頑張りましょう。
問題 三角形の二等分
以下に示すのは本記事で取り組む三角形の二等分に関する問題です。

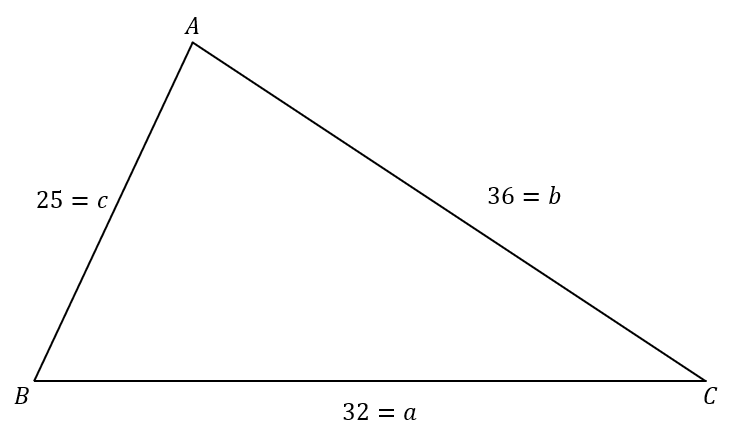
この問題を例に解説します。
難しい問題かもしれませんが頑張りましょう。
問題を解く前の下準備
まずは、問題を解く前の下準備と方針を決めます。
辺の長さについて、「BC=32, CA=36, AB=25」です。
数学が出来ないやつはこの値をそのまま代入して求めようとします。
ところで、昔書いた記事でも触れたと思いますが、図形量の最大値や最小値の問題は変数をおけるかどうかが鍵になってきます。
何を変数におくのかと聞かれたら「長さ or 角」のどちらかです。
本問は数値をそのまま代入すると計算がだるいです。
そのため、辺の長さを文字で置く「数値の文字化」という技を用います。
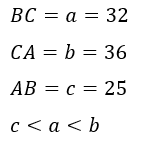
また、辺上に取る任意の2点をD,Eとします。
準備ではDはAB上の点、EはAC上の点とします。
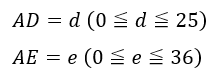
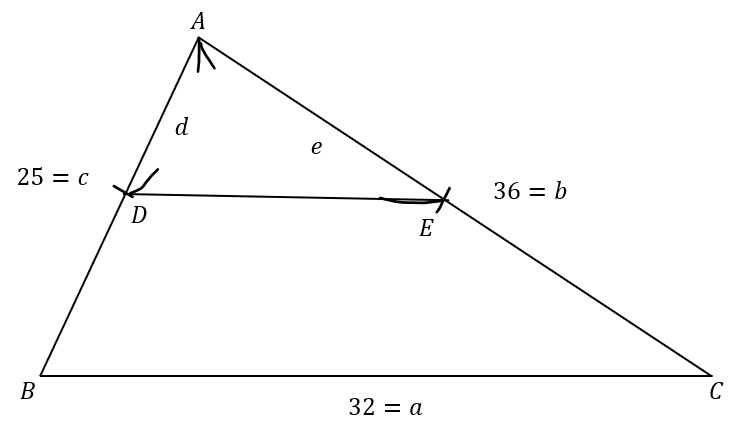
ここで、三角形ABCの面積はADEの面積の2倍です。
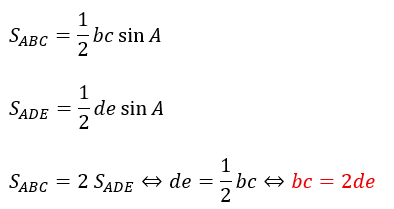
また、余弦定理を用いると・・・
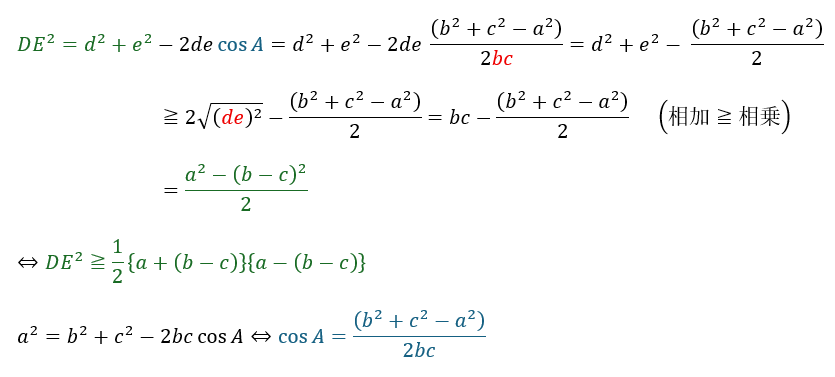
相加相乗平均に関する記事はこちらです。
上の緑の不等式は点がABとAC上にあるときに成立する不等式ですが、「BA,BC上にあるとき」や「CA,CB上にあるとき」も同じように不等式を作成できます。
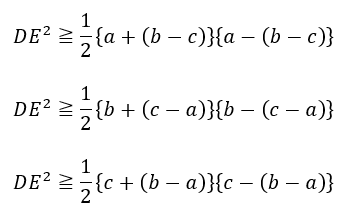
上のように3種類の不等式が出来ます(これが答えみたいなモノ)。
点をAB,ACにとる (角Aを起点とする)
最初から愚直に求めると答えは以下のようになります。
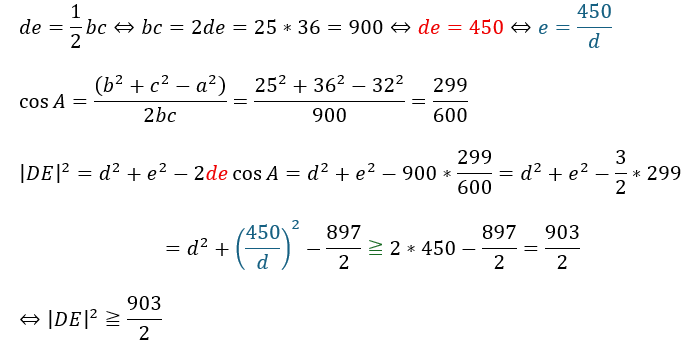
緑の≧の右辺と左辺で相加・相乗平均を用いています。
これは、準備段階で求めた不等式の内の1つで実際に・・・
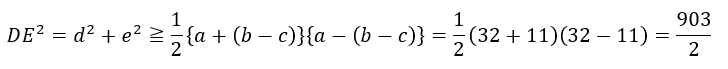
角B・角Cを起点にする (他の辺上にある)

上の緑の不等式は青の等式が成立する前提で成り立っています。
結論
以上の議論から線分の値が最小になるときは、点をCAとCBに取るときで、以下の不等式が成立します。
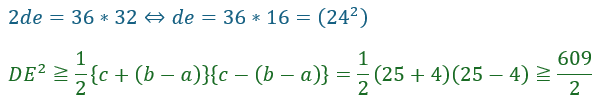
以上から、DEの長さが最小になるのはCD=CE=24 (E≠D)となるような場所にDとEがあるときです。
上の線を引いたところは重要です。こういうことに言及するかしないかで差が出ます。



コメント