こんにちは。Horyです。
今回の記事では万有引力と天体運動について解説します。
惑星がどのような運動を行うかをケプラーの法則などの説明も交えて原理と本質から解説しようと思います。
ちなみに、重力に関しての記事で万有引力についても触れているので是非こちらの記事にも目を通しておいてください。
今回も頑張りましょう。
万有引力と位置エネルギー
まずは、万有引力についてです。
2つの物体には大きさや距離に関係なく互いに引きつける力が働いています。これを万有引力と言い、力の大きさは以下のように書けます。
ここでは、2つの物体の質量をそれぞれ、m,Mとし、2物体間の距離をrとします。

ここで、Gは万有引力定数と言われるモノです。
また、重力は万有引力の一種で地球表面での万有引力について、運動方程式に代入したときの加速度を一定とみなし、これを重力加速度gとしていました。
これは前回の記事の内容の復習になります。
ところで、重力は保存力の1つであることをこの記事で話しました。
重力は万有引力の一種です。重力が保存力であるなら、万有引力も保存力の1つです。
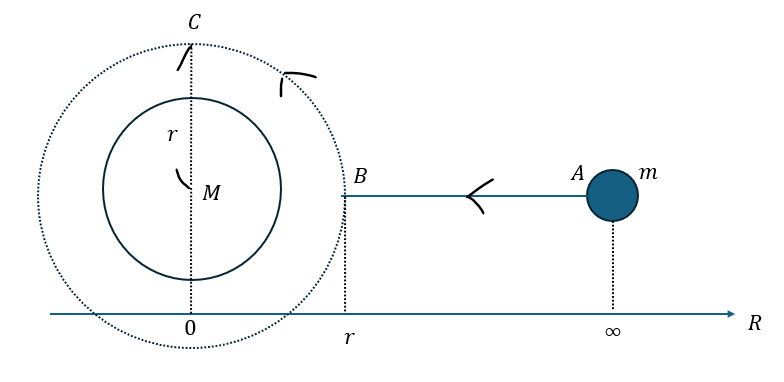
万有引力について、物体(人工衛星とか)が以下のようなルートをたどるとして万有引力による位置エネルギーを求めてみましょう。
ちなみに、万有引力の基準点は無限遠方です(無限に離れた点で位置エネルギーが0になる)。
物体がA→B→Cのルートをたどるときの位置エネルギーを求めます。
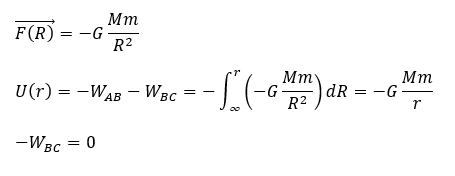
天体の運動とケプラーの法則
天体の運動とケプラーの法則についてデス。
以下の3つの法則について個別に解説します。
- ケプラーの第1法則
- ケプラーの第2法則
- ケプラーの第3法則
覚えておくと良いことですが、ケプラーの法則は楕円軌道の時しか使いません。
また、簡単のために「第2法則→第1法則→第3法則」という順に説明します。
また、運動方程式の極座標変換を用いるのでこの記事の内容を理解しておいてください。
また、極座標表示の動径方向と接線方向の運動方程式は頭に入れておいてください
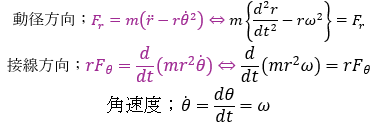
ケプラーの第2法則
ケプラーの第2法則とは、「恒星の周囲を運動する惑星について、惑星と恒星を結ぶ線が掃く面積速度が一定という法則」です。
これについて証明します。
まず、惑星に働く力は恒星に向かう万有引力のみです。これは中心力と言えるので、角運動量保存則が成立します。
角運動量保存則については、こちらの記事で少し触れているので読んでおいてください。
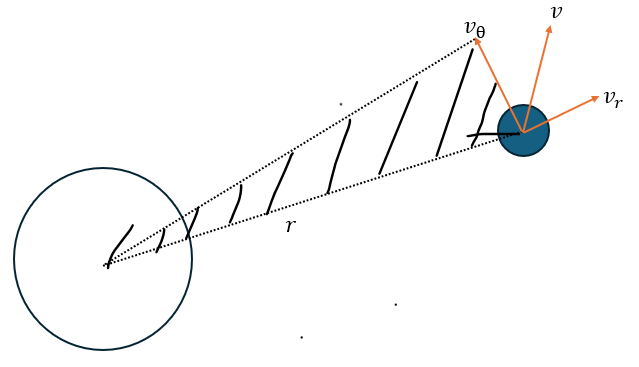
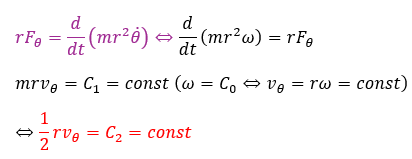
上の赤く示した式が面積速度一定の式です。図おける斜線を引いた部分の三角形の面積が定数になるという公式です。
ケプラーの第1法則
ケプラーの第1法則とは「惑星が恒星を焦点とする楕円軌道をとる」という法則です。
この法則が成立することを証明します。以下に図を示します。力については大きさで記述しています。
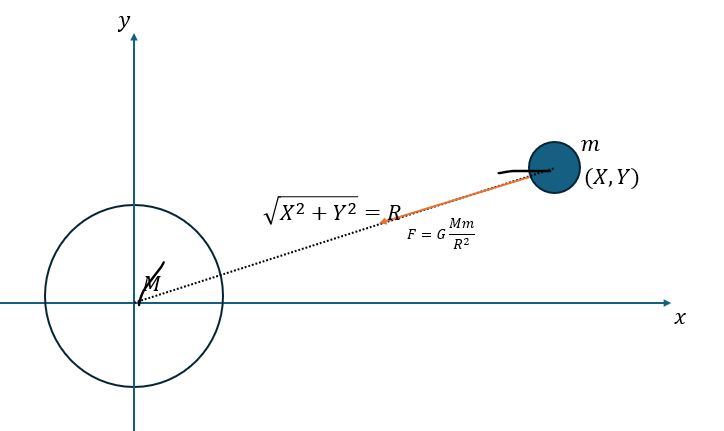
極座標における動径方向の運動方程式を記述します。
また、第2法則の議論から接線方向の運動方程式は0になります。

上の赤い式で書いた微分方程式を解けばいいわけです。
まぁ、これの計算については一々やっていると頭が痛くなるので省略します。もしも、求めたい人は調べてみてください。最終的にrは以下のように書けます。
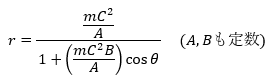
こちらの記事でもやりましたが、これは二次曲線を極座標表示したときの式と一致します。
ケプラーの第3法則
ケプラーの第3法則とは、惑星の公転周期をT[s]として、楕円軌道の長半径をaとすると、公転周期が以下のように記述できることです。
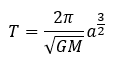
これを証明してみます。ただし、この法則は近似をたくさん使います。(楕円軌道で近似的に軌道の半径は一定と見なしてあげます。)
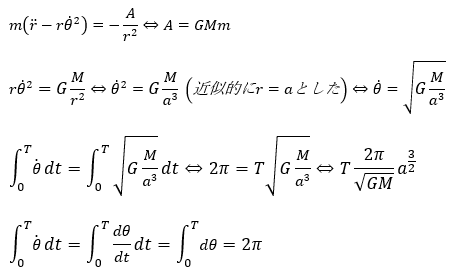
以上により証明できました。次回から練習問題に移ります。



コメント