こんにちは。Horyです。
前回の記事では波動の種類と横波・縦波の違いについて簡単に解説しました。
今回の記事では一次元波動方程式の解を導きたいと思います。
この解を導くには微分方程式を解く必要がありますが、この微分方程式の解のことを物理ではダランベールの解と呼んでいます。
今回も頑張りましょう。
一次元波動方程式について
一次元の直線に表現できる波動は以下のような式に表すことが出来ます。
というか、高校に出てくる波動方程式は全て以下のように表すことが出来ると言っていいです。
ここで、パラメータを以下のように定義します。
- u (x,t);媒質の変位 (位置と時間の二変数で定義される)
- C;定数
以下に示すのは一次元波動方程式の微分方程式です。
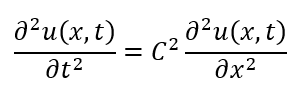
二変数の微分方程式なんて解けるのか、、、と思うかもしれませんが工夫すれば解くことが出来ます。
ダランベールの解
上に示した微分方程式の解を導きます。
しかし、このままでは難しいので新しく変数を設定します。
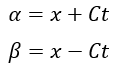
このように設定してu(x,t)→u(α,β)として考えます。
別にxとtは用いているので変数が変わっても問題はないです(同じ微分方程式であることに変わりはない)。
ここで、二変数関数の偏微分を用います(下の立式は合成関数の微分を応用したモノで成り立つことが分かっている)。
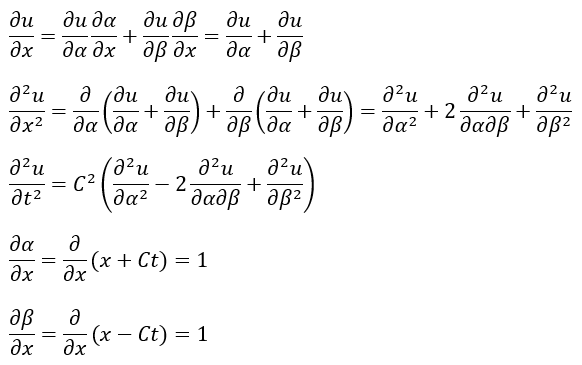
上の式を元の微分方程式に代入してみます。
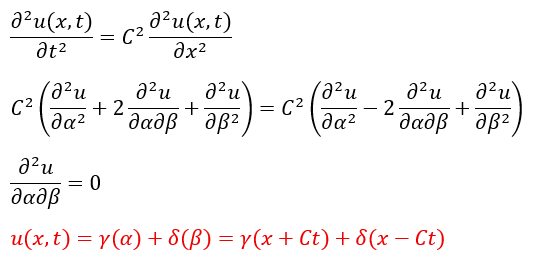
ここで、γとδはαとβで表される任意の関数です。
上の赤い式で書かれた部分が微分方程式の一般解でダランベールの解と呼ばれているモノです。
一般解の意味
上で導出した解の意味を考えてみます。
- δ(x-Ct);u =δ(x)の波動が「+x方向」に速さCで動く
- γ(x+Ct);u =γ(x)の波動が「-x方向」に速さCで動く
勘違いする人が多いのが、速さCというのは波の形の動く速さであって、物体の動く速さではないです。
そのため、波の動く速さのことを物理では位相速度と言います(これは注意してほしいです)。
また、一次元波動については2つの大きな規則があります。
- 規則 ①;波動の形
- 何もない場所で波動が発生
- 形状を変えずに等速度で移動する
- 位相速度は媒質の種類と状態に依存 (空気と水とかでは全く違う)
- 貴族 ②;2つの波動
- 2つの波動が重なる
- 重なった点の変位は2つの波動の変位の和 (重ね合わせの原理)
特に、重ね合わせの原理については以下の図に表すように書けます。
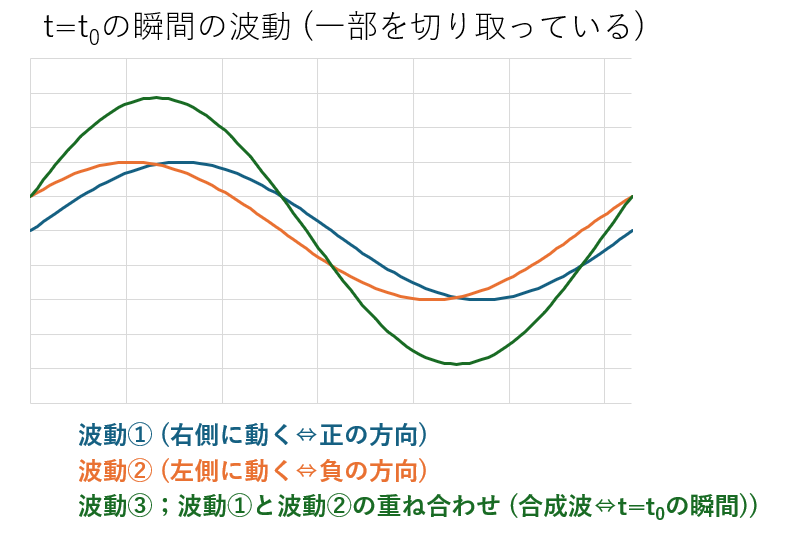
緑の波動は青い波動とオレンジの波動の重ね合わせです。
注意してほしいのは、上に書いた波はある時刻「t=t0」での波を書いたモノで、常に上の図のような状況ではありません。
理湯は波動①も波動②も常に変位するからです。



コメント