こんにちは。Horyです。
今回の記事では、電磁気学でよく使う技術のラプラス方程式とポアソン方程式について簡単に解説します。
今回の記事は完全に大学内容なので、読み飛ばしたい方は読み飛ばしても構いません。
ただ、この記事の内容が理解できていないと次の記事で解説するビオサバールの法則の原理を理解できなくなります。
また、この記事では微分演算子が出てきます。微分演算子の記事はこちらです。
今回も頑張りましょう。
電場の定義 復習
電場の定義をもう一度復習します。高校物理では電場は大きさとして表示されることが多いですが、本来はベクトルです(向きと大きさを持つ)。
n個の電荷Q1,Q2・・・Qnの電荷の位置をr1,r2・・・rnと置きます。
このn個の電荷が位置rに作る電場をベクトル表示すると・・・

各電荷が作る電場をベクトル的に足し合わせています。ここまでは、前回の記事の復習になります。
静電場とラプラシアン
微分演算子の中にラプラシアンがあります。これは前回の記事で説明していませんでした。
ここで、ガウスの法則を考えます。
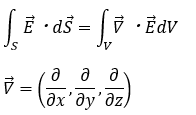
いつもは、この式の左辺が単位体積当たりの電荷密度を真空の誘電率に等しい(電気力線の数に等しい)というようにして電場を求めていました。
今回はこの式の右辺に注目します。
ここで、静電場について、div (発散)とrot (回転)を考えます。
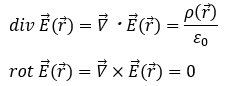
静磁場の場合も磁束密度の回転は0になりましたが、静電場の場合も電場の回転は0になります。今回は証明しませんが、これは成立します。
ここで、電位をφ(いつもはVにしてますが、体積記号と被る)とすると・・・
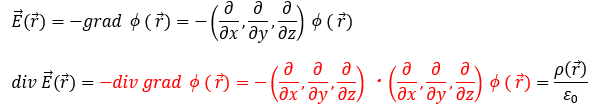
上の赤い部分の意味は「∇の電位倍(ベクトル)」後に「∇の電位倍に∇を内積(ベクトルの内積/スカラー)しています。
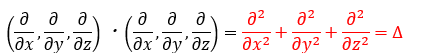
上の式の赤い部分を△で表してラプラシアンと呼んでいます。ラプラシアンはスカラー量です。
だから・・・
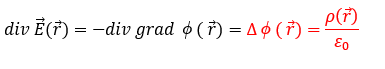

ラプラス方程式は電荷密度が0の時に電位のラプラシアンを取った値が0になるときです。
ポアソン方程式を解く
ポアソン方程式を解いていきます。
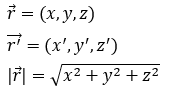
電場の式から電位を求めます。
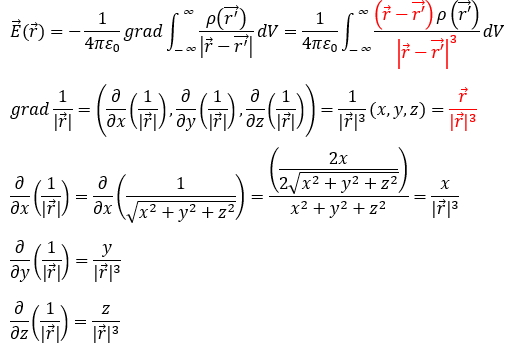
上の式は成立していることが分かると思います(ベクトルは簡易なものにしたが・・・)
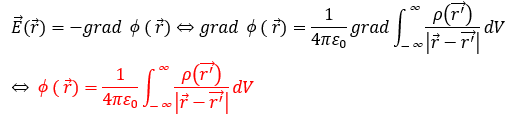
ポアソン方程式を解くことができました。上に書いた赤い部分を次回の記事で使います。よく覚えておいてください



コメント