こんにちは。Horyです。
これまでに電磁気学の様々な現象を解説してきましたが、電磁気学の原理はマクスウェル方程式です。
今回の記事では電磁気学の原理であるマクスウェル方程式について解説すると共に、4つの式が登場すると思いますが、これらの意味を数学的視点と現象的視点から解説していこうと思います。
また、マクスウェル方程式の微分系と積分系もこの記事でまとめます。
今回の記事は結構しんどいかもしれませんが頑張りましょう。
マクスウェル方程式
マクスウェル方程式は4つ存在します。
その前に、登場する文字の定義をしていきたいと思います。

式に出てくる文字を上のように定義できると考えます。
マクスウェル方程式に出てくる原理は以下の4つです。
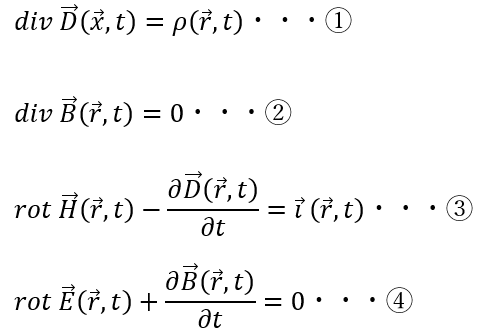
①~④の式を合わせてマクスウェルの方程式(微分系)と呼びます。
divやrotの微分演算子に関してはこちらの記事を読んでおいてください。
- ①;ガウスの法則 (空間での静電場・・・真空でも物質中でも)
- ②;ガウスの法則 (静磁場)
- ③;マクスウェル・アンペールの法則
- ④;フィラデーの電磁誘導の法則
- 静電場・・・時間変化しない電場 (時間変化しない定常電流が流れる)
- 変位電場・・・時間変化する電場 (時間変化する変位電流が流れる)
- 静磁場・・・時間変化しない磁場
- 変位磁場・・・時間変化する磁場
ガウスの法則
ガウスの法則について簡単におさらいします。
実は、ガウスの法則についてはこちらの記事でも解説したので記事を読んでおいてください。
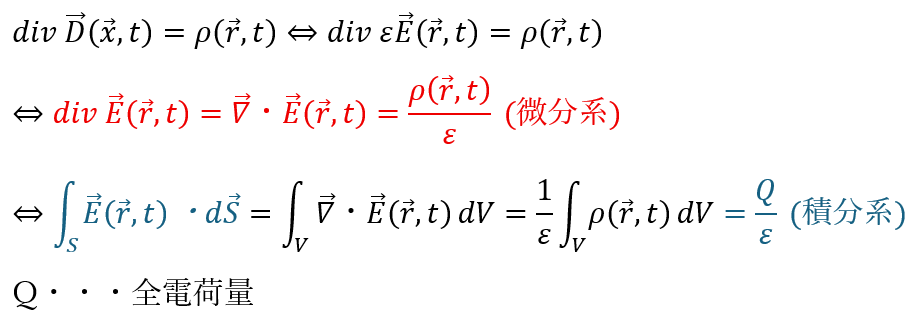
赤い部分ですが身に覚えのある形ですね。
- 数学的意味 (微分系)
- 左辺;電場ベクトルの発散 (電場をx,y,zで内積的に偏微分する)
- 右辺;電荷密度を誘電率で割った値 (単位体積の電荷に関する電気力線の本数)
- 結論;電場ベクトルの発散は単位体積当たりの電気力線の本数
- 数学的意味 (積分系)・・・青い部分を使う
- 左辺;立体の表面積を垂直に貫く電場の量 (立体内から湧き出る電場の量)
- 右辺・・・全電気量を誘電率で割った値 (電気力線の本数)
- 結論;立体内から湧き出る電場の量は電気力線の本数に等しい
- 物理的意味
- 電気量をもつ物体は必ず電場を発生させる (真空中でも物質中でも)
ガウスの法則 (静磁場)
静電場のガウスの法則を解説します。
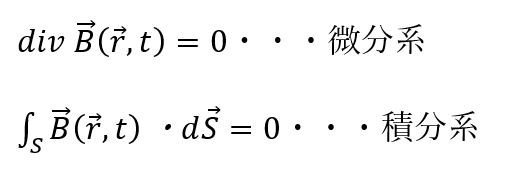
- 数学的意味
- 左辺;磁束密度の発散 (磁束密度をz,y,zで内積的に偏微分する)
- 右辺;0である
- 結論;磁束密度の発散は0である。
- 物理的意味
- 磁石はS極とN極で必ずペアになっている。
- どれだけ細かくしてもSとNを分離することは不可能
- 磁力線は必ずループする
ちなみに、上に示す磁束密度を具体的にどうやって求めるかと言うのがビオ・サバールの法則になります。
ビオ・サバールの法則は以下の記事に証明してあるので読んでおいてください。
円電流と直線電流が作る磁束密度は暗記で良いかもしれませんが、どのようにして求めるかの原理は知っておいた方が良いです。
マクスウェル・アンペールの法則
マクスウェル・アンペールの法則を解説します。
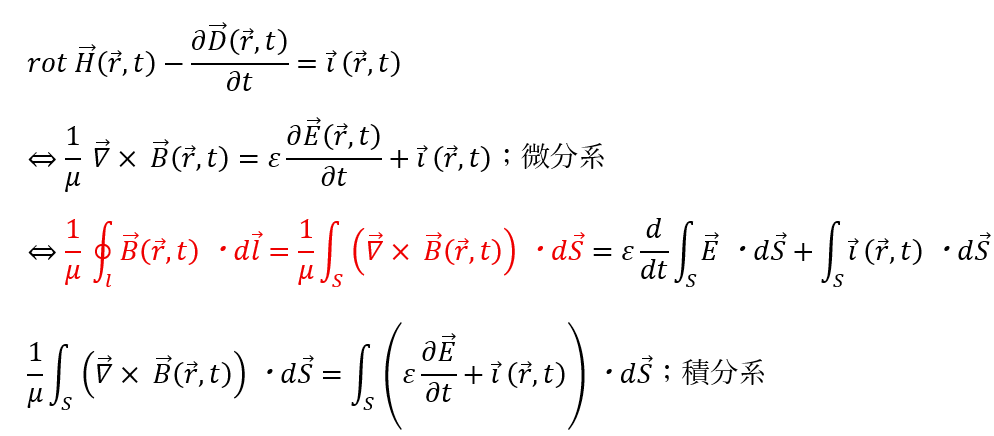
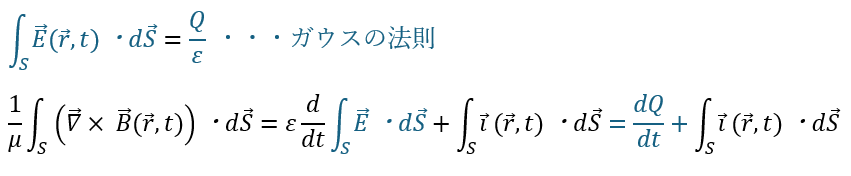
赤い部分はストークスの定理を用いています。
ストークスの定理とそれを応用したアンペールの法則に関してはこちらの記事に詳しく書いてあるので読んどいてください。
電流の正体は電荷の流れでアルコとを考慮すると上の電場の式の部分も納得できますよね・・・
- 数学的意味
- 左辺;磁場の回転 (磁場にx,y,zで外積的に偏微分する)
- 右辺;電場の時間変化と電流密度の和
- 結論;磁場の回転が電場の時間変化と電流密度の和
- 物理的意味
- 磁場が存在すれば電場が発生し電流が流れる
- 磁場が時間変化しない静磁場なら時間変化しない定常電流の発生
- 磁場が時間変化する変位磁場→変化に対応する変位電場→変位電流の発生
- 右ネジの法則も説明できる
ファラデーの電磁誘導の法則
ファラデーの電磁誘導の法則を解説します。
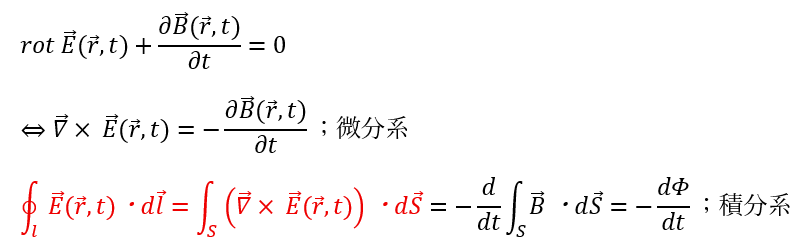
赤い部分はストークスの定理で、Φは磁束を表しています。
ファラデーの電磁誘導の法則は以下の記事でも解説しています。
- 数学的意味
- 左辺;電場の回転 (磁場にx,y,zで外積的に偏微分する)
- 右辺;磁場の時間変化に-1を掛けた
- 物理的意味
- 時間変化する変位電場が流れると磁束が発生する。
- それは電場の変位を妨げる向きに発生する (偏微分にマイナスが付いている理由)
- 妨げる・・・生成した磁束にマクスウェル・アンペール則を適用
- ⇒反対向きに電場が発生⇒妨げる



コメント