こんにちは。Horyです。
今回の記事では大学の熱力学で非常に重要な公式の1つであるマクスウェルの関係式に関して解説します。
マクスウェルの関係式とマクスウェル方程式で混同する方もいると思いますが・・・
- マクスウェル方程式・・・電磁気学の基本原理
- マクスウェルの関係式・・・熱力学の偏微分に関する公式
上の2つを混同しないように気をつけてください。
今回も頑張りましょう。
偏微分に関するルール
マクスウェルの関係式を解説する前に偏微分に関するルールを解説します。
偏微分に関する記事はこちらの記事に書いたとおりです。今回はもっと深い偏微分のルールを解説します。
熱力学で出てくる関数を熱力学関数と呼びます。
関数が連続や微分可能と言うことについては下に示す記事にも書いたとおりです。
n回微分可能である関数をCn級関数と呼びます。
ここで、関数が2回微分可能なC2級関数の偏微分について以下のことが成立します。
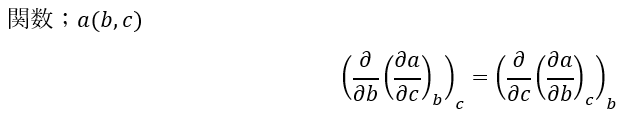
上の式の意味を解説します。
- 左辺について・・・
- 関数aについて変数bを定数と見てcで偏微分する
- 上で偏微分したものについて、変数cを定数と見てbで偏微分する
- 右辺について・・・
- 関数aについて変数cを定数と見てbで偏微分する
- 上で偏微分したモノについて、変数bを定数と見てcで偏微分する
- 結論
- 左辺と右辺は等しい
- 偏微分の順番は結果に影響しない(C2級関数であれば・・・)
まぁ、これの証明は大学の微分積分学という授業で触れると思います(僕のやる気があれば記事にすると思います)。
このことを利用してマクスウェルの関係式を導出したいと思います。
マクスウェルの関係式
マクスウェルの関係式を証明していきますが、型が4つあるので個別に解説します。
- 基本形 (まぁ、オーソドックスな形)
- エンタルピーが与えられる
- ヘルムホルツの自由エネルギーが与えられる
- ギブスの自由エネルギーが与えられる
基本形の導出
熱力学第一法則をエントロピーで表していきます。
系を主役にして吸収熱量、気体がする仕事を正にします。

ここで、青い式の両辺をSを定数と見てVで偏微分します。
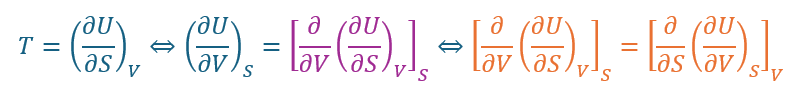
そして、緑の式の両辺をVを定数と見てSで偏微分します。
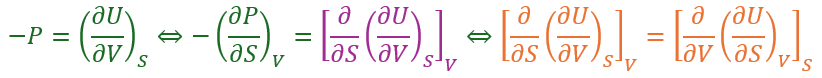
上の式の紫の部分は順序を入れ替えても変わらないのでオレンジのように変形できますが、オレンジの部分は同じですよね。
だから、以下の式が成立します。
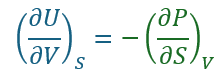
上の式がマクスウェルの関係式の基本形です。
エンタルピーが与えられる
エンタルピーHが与えられた場合を考えます(エントロピーではないです)。
エンタルピーは定圧条件での熱量変化を定義しやすいです。
まぁ、やることは同じです。

ヘルムホルツの自由エネルギーが与えられる
ヘルムホルツの自由エネルギーFが与えられる場合のマクスウェルの関係式を導出します。

ギブスの自由エネルギーが与えられる
ギブスの自由エネルギーGが与えられる場合のマクスウェルの関係式を導出します。




コメント