こんにちは。Horyです。
前回の記事では半導体の基本的性質を理解するとともにn型とp型を組み合わせて作る電子機器;ダイオードの整流作用に関しても解説しました。
今回の記事では前回の記事に関連してホール効果についてまとめようと思います。
今回も頑張りましょう。
ホール効果
以下に示す図を考えます。
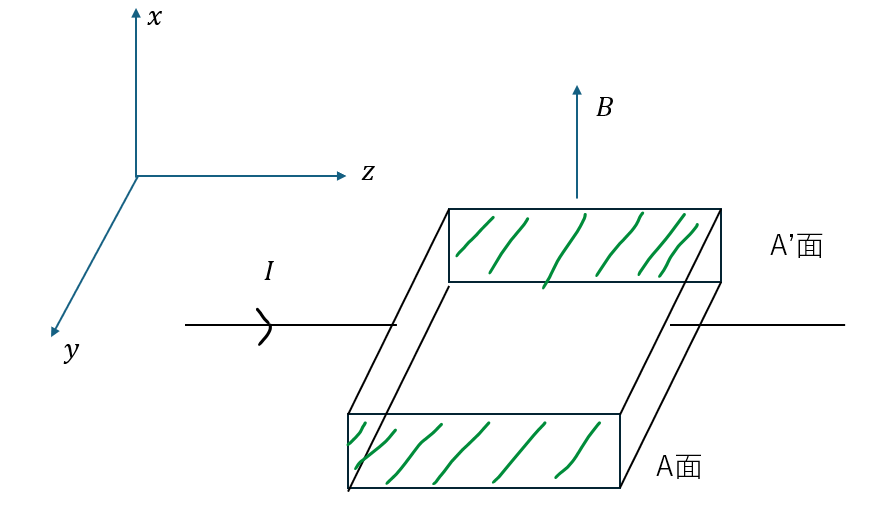
19世紀後半に磁場中に置いた導体へ図の向きに電流を流すとA面とA’面間に電位差が生じる現象が発見されて、これをホール効果といいます。
何でこんなことが起きるのかというと・・・
今は電気量q>0として考えます。
電気量qを持つ電荷がy-z平面でどのようになっているかを考えます。
電流があるということは起電力を持った電池に接続されているということです。
そのため、+z方向に電場が発生して電場より力を受けます。
電場だけではありません。磁場があるということはローレンツ力も電荷は受けます。
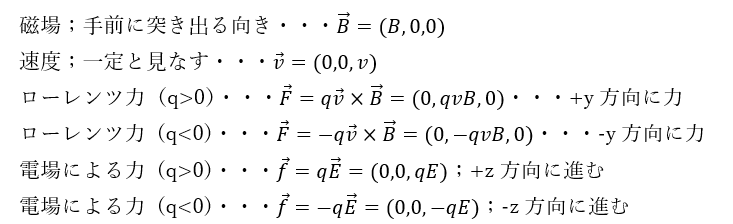
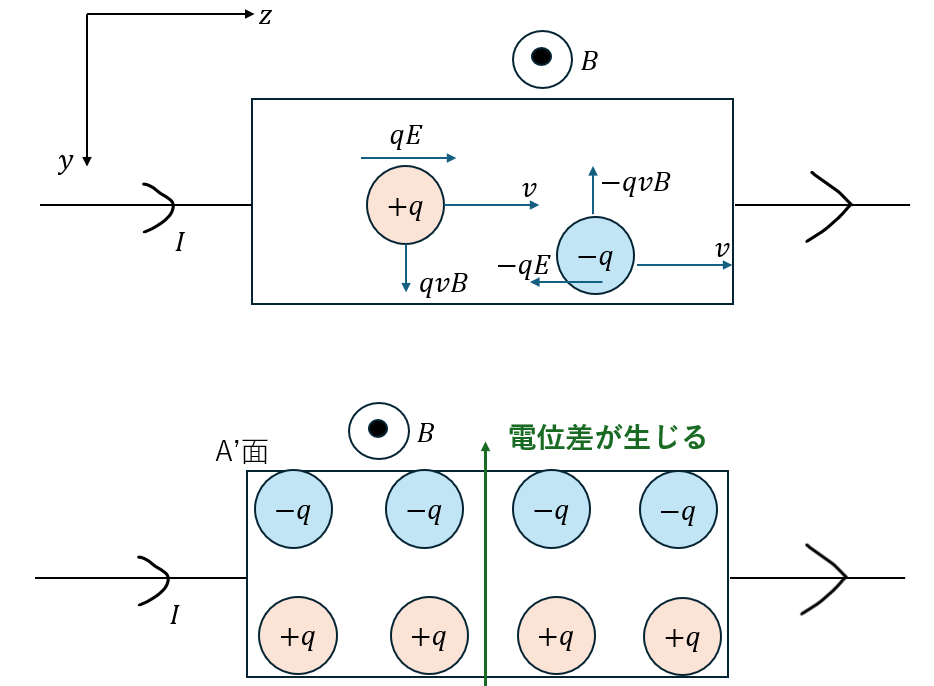
ここで、重要なのはローレンツ力の向きです。
- 正の電荷・・・+y方向にローレンツ力
- 負の電荷・・・-y方向にローレンツ力
- A面・・・正電荷が集まる
- A’面・・・負電荷が集まる
- y方向;ローレンツ力によって面に集まる電荷に偏り→電場が発生し電位差
- z方向;電池の起電力による電位差
このようにローレンツ力により電荷の偏りが生じ電位差が発生することをホール効果といいます。
半導体の種類による電位差
先ほどの図で考えます。
面A’の電位を0Vとしたときに面Aの電位は直方体の素材が変わることによってどうなるかを考えます。
- 試料の種類
- 金属
- n型半導体
- p型半導体
重要なのは上の3つの試料に電流を流すと何が動くかということが重要です。
- 金属;自由電子が動く→マイナスの電荷→Aの電位は負
- n型半導体;15族の余った電子が動く→マイナスの電荷→Aの電位は負
- p型半導体;13族の電子の空席が動く→空席は正電荷とみなす→Aの電位は正
運動しないときの電場
運動が止まるときの電場を求めてみましょう。
どういうことかというと、電荷が受けるローレンツ力と電場から受ける力が釣り合うということです。
電荷が正でも負でも導ける式は変わりません。仮に、その時の電場をEqと置くと・・・
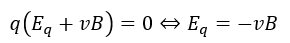
面A’の電位を0Vとしたときの面Aの電位を求めてみます。
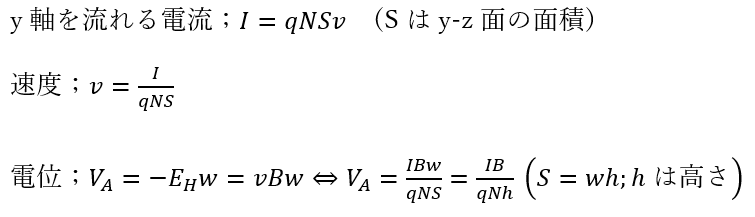
最後に宿題を出します。
半導体と導体でどちらの方の電位差が大きくなるか考えていただきたいです。



コメント