こんにちは。Horyです。
前回の記事では荷電粒子を加速するための装置であるサイクロトロンの原理を解説しました。
今回の記事ではベータトロンと言う装置の原理を解説するとともに謎を解明したいと思います。
今回も頑張りましょう。
ベータトロン
ベータトロンのベータは「β線」のベータです。
物理でベータ線は電子を意味します。つまり、この装置は電子を加速する装置です。
装置の模式図を以下に示します。
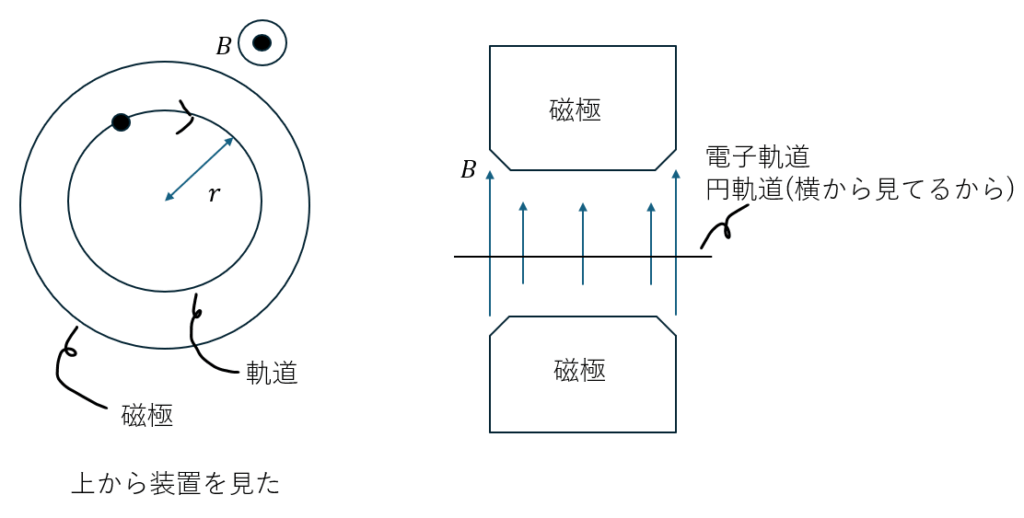
上図に示すように二つの磁極内には磁場が発生します。
そして、重要なのがこの磁場は静磁場ではなくて変位磁場です。
ファラデーの電磁誘導の法則でも話しましたが、磁場が変位するとそれに対応して誘導電場が発生します。
磁極内の電子は電磁誘導による誘導電場によって加速されるわけです。
ベータトロン中の電子は半径を変えることなく誘導電場で加速し続けます。
ここで、勘のいい人は気づくかもしれませんが、「半径を変えることなく加速するのって無理じゃね…」と思います。
- 加速させる方法
- 磁場を大きくする
- 誘導電場が大きくなる
- 電子が加速する
- 電子の速度が大きくなる
- 軌道半径も大きくなる
「半径変えずに加速するの無理やん!」と思うかもしれませんが、実際のベータトロンでは半径を変えずに運動します。
どこかで何らかの工夫をしていると考えれます。
以下ではこの工夫を解明しようと思います。
以降では半径が一定と考えてrは定数とみなします。そのため、rは微分も積分もされません。
誘導電場を求める
ファラデーの電磁誘導の法則を用いて誘導電場を求めてみます。
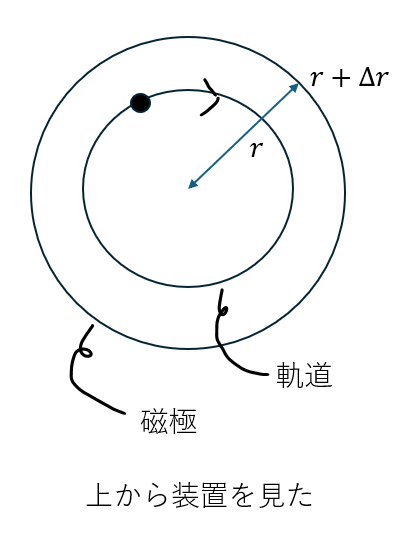
半径rからr+Δrにおける磁束の微小変化を求めてみたいと思います。
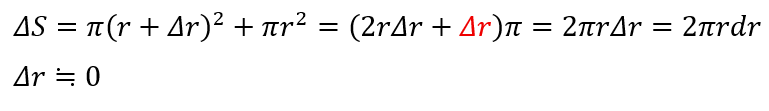
赤い部分はあまりにも小さいので物理では無視しでいいです。
続いて、ΔSの部分を貫く微小磁束を求めてみます。
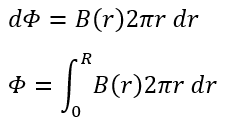
ここで、ファラデーの電磁誘導の法則を用います。
単位長さ当たりの電場をEと考えると、円周のため、誘導起電力は容易に求められます(誘導起電力をVとする)。
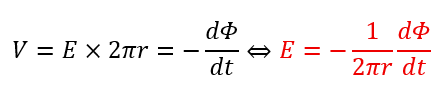
誘導起電力の向きは磁場の変化を妨げる向きに流れます(電子が加速する方向と反対の方向)。
上に示した式を後に使います。
運動方程式を考える
運動方程式を考えてみます。
電子は円運動を行っているので中心方向と接線方向で二つの運動方程式を記述します。
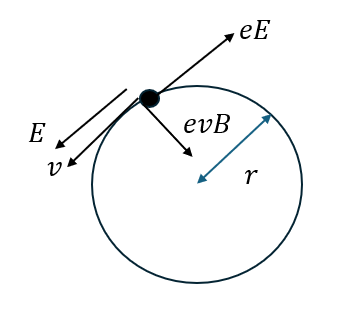
電子であることに注意していただきたいです。電子は-の電荷を持ちます。
図は「力の大きさ(文字)」と「ベクトル」を分けています。
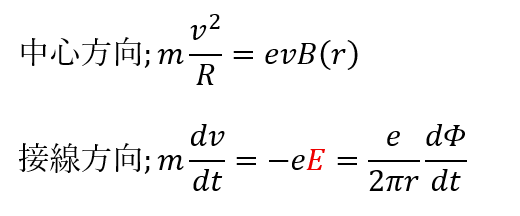
ファラデーの電磁誘導の法則により紙面を突き出る向きに増加する磁場を妨げる向きに誘導電場が発生します。
右ネジの法則で紙面の奥に進む磁場を増加させるにはどの向きに電場をかけるかよく考えてみてください。
半径一定の謎
接線方向と中心方向の運動方程式から速度を求めます。

上の式のオレンジの部分を連立してみます。
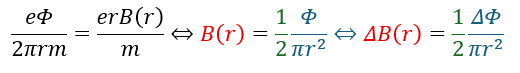
上の式で色がついてる部分は半径が一定で電子を円運動させるための条件です。
- 赤い部分・・・電子の軌道上の磁束密度
- 青い部分・・・軌道内の磁束密度平均
- 緑の部分・・・半分にしている
半径を一定にして電子を運動させたいのなら「回路を貫く磁束密度平均の増加の半分だけ電子軌道上(円周上)の磁場を増価させろ」というのが結論です。



コメント