こんにちは。Horyです。
前回の記事では電磁気学の導入記事として電磁気学と力学の違いに関して簡単に解説すると共に場の概念について話しました。
今回解説するのは大学における物理数学の分野になりますので、この記事を読みたくない人は読み飛ばしていただいて構いません(理系の人は読んでほしいな(願望))。
大学の電磁気学において、場の概念は非常に重要です。これを理解するためにベクトルとスカラーの違いは必ず理解しなくてはなりません。
以下の記事にも触れましたが・・・
- スカラー・・・大きさのみを持った量(単なる数値)
- ベクトル・・・向きと大きさを持った量
そして、数学におけるベクトルとスカラーを簡単にまとめます。
- 座標・・・ベクトル
- 座標成分・・・スカラー (1,2,3)とかのx成分1とか
- ベクトルの和や差・・・ベクトル
- ベクトルのスカラー倍・・・ベクトル
- ベクトルの内積・・・スカラー
- ベクトルの外積・・・ベクトル
これらが何故そうなるかについてはこちらの記事に詳しく説明してあるのでご確認ください。
ベクトル場とスカラー場
ベクトル場と言われてもピンとこないと思いますが、定義通りに説明すると、座標空間における座標にベクトル関数を指定することでベクトル場を与えたといいます。
どういうことかというと、私たちが今までに数学や力学で扱ってきたベクトルは中身(成分)が変化しないベクトルでした。ただ、大学の物理になるとベクトルの向きや大きさが時間や位置によって変わると言うことです。
時間や位置によって変化するベクトルをベクトル関数と言います。以下に簡単な例を示します。

まぁ、ここまでやってもピント来ないと思うので、具体例を示します。

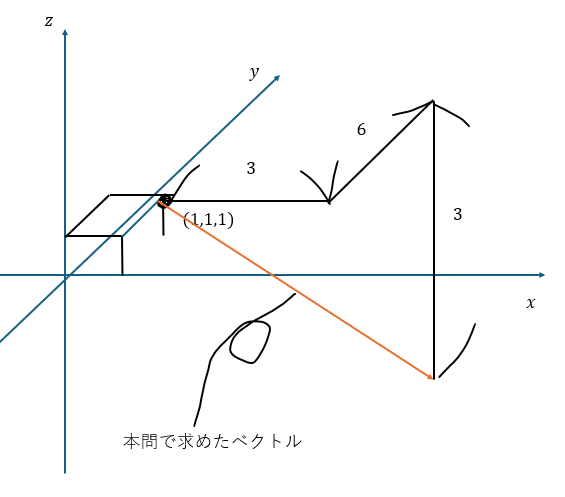
これは座標(1,1,1)で(3,6,-3)の方向のベクトルを持っているということができます。
日常の例で考えると気流はベクトルになります。気流の向きと大きさが時間によってどのように変化するかと言うこともベクトル関数で表すことができます。
ただ、気流の向きや大きさも位置によって変わります。場合によってはベクトル関数の中にベクトルがある場合も考えられますね。
一方でスカラー場は座標空間の座標にスカラー関数を指定することでスカラー場を与えたと言います。どういうことかというと・・・

つまり、座標(3,2,1)で大きさ8のスカラー量を持っていると言うことができます。
ところで、ベクトルが時間や位置によって変化する関数のように扱えるということは・・・ベクトルも微分することができますね。
ベクトルを微分するときに必要になる技術が演算子というものです。
これから大学で学ぶ基本的なベクトル(微分)演算子を解説するので数学的意味を正しく覚えてください。
ベクトル演算子 まとめ
以下に今回の記事で解説するベクトル演算子を簡単にまとめます。
- grad・・・勾配 (グラディエント)
- ∇・・・ナブラ (これだけ覚えても良い)
- div・・・発散 (ダイバージェンス)
- rot・・・回転 (ローテーション)
これらについて解説します。どれも電磁気で非常に重要な演算子になります。
ここで、ベクトル関数とスカラー関数を以下のように設定します。
これらを上の演算子に作用させたときの結果と数学的操作を言葉で説明できるようにしてください。
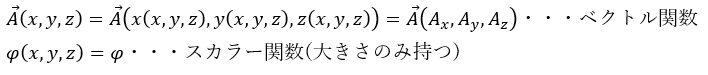
gradとナブラについて
偏微分についてはこちらの記事を読んでおいてください。

divとナブラ

rotとナブラ
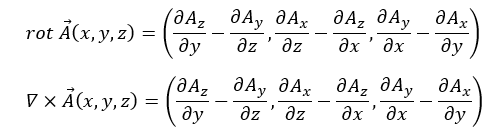
ナブラにベクトル関数を外積で作用させるとベクトルになり、ベクトル関数にナブラの外積とrotを作用させたモノは同じ結果になる。
まとめ・・・
以下は学んだ事のまとめです。
- ナブラはベクトルにもスカラーにも作用が可能
- スカラー関数にナブラを作用させたモノはgladを作用させたモノと同じ
- ベクトル関数にナブラを内積したモノはdivを作用させたモノと同じ
- ベクトル関数にナブラを外積下モノはrotを作用させたモノと同じ
- gladはスカラーに作用させるもの
- div,rotはベクトルに作用させるもの



コメント