こんにちは。Horyです。
整数分野で教科書には発展的内容として掲載されているかもしれませんが、フェルマの小定理と呼ばれる定理があります。
フェルマの最終定理がなければこの定理が小定理と呼ばれることはありませんでした。
僕は、この定理のことを「フェルマの最終定理の被害者」と呼んでいます。
フェルマの小定理は入試でもたまに出るので知っておいた方が良いです。
今回はこの定理の証明に関して解説します。
今回も頑張りましょう。
フェルマの小定理
フェルマの小定理とは素数と倍数に関する定理のことで、以下に示すとおりです。
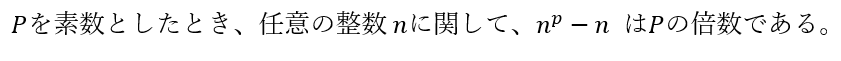
これがフェルマの小定理です。
証明方法は私が思いつく限りは2つあります。
- 組合わせを用いる方法
- 割った余りに注目する方法
以上の2つの方法を個別に解説します。
組合わせを用いる方法
最初に紹介する方法は組合わせを用いる方法です。
- pCkがPの倍数であることを証明する (k=1,2,・・・P-1)
- 数学的帰納法で小定理を証明 (二項定理が出る)
上の二段階で証明します。
数学的帰納法の記事は以下の通りです。
以下は証明です。
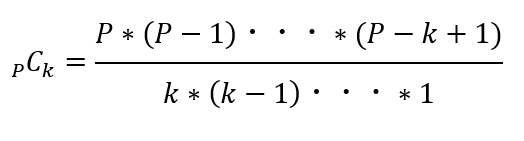
- 分子;PがあってPは素数なので1と自分以外に約数なし
- 分母;k≦P-1⇔Pを素因数に含む数がない
- 結論;分子のPは約分されずに残る・・・Pの倍数
つづいて、数学的帰納法を用いて小定理を証明します。

以上からn=m+1のときも成立するので数学的帰納法により小定理が成立することが証明されました。
割った余りに注目する方法
二つ目の方法が割った余りに注目する方法です。
文字を以下のように定義します。
- P・・・素数
- Q・・・Pと互いに素な数
- Rk・・・PをQk (kは1~P-1の自然数)で割った余り (余りはP-1個)
以下の4ステップで証明します。
- 余りが0になることはない (割り切れない)
- P-1個の余りは全て異なる
- P-1個の余りに1,2・・・P-1が一個ずつ登場
- 小定理の証明
最初の2ステップは背理法で証明します。
背理法の記事は以下に示すとおりデス。
以下は割り切れないことの証明です。

以上の二点から矛盾してしまうので余りは0になり得ません。
次に、余りが全て異なることの証明です。

以上の二点から矛盾してしまうので余りは全て異なります。
上の式の3段目がよく分からない人は実際に式を書いてみれば良いです。
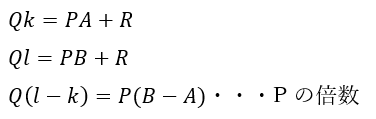
つづいて、余りに1~P-1が余りに1つずつ登場することの証明です。

これらの3ステップを用いることで小定理を証明できます。
最後に小定理を証明します。

- 赤い部分;QがP-1個掛け算されてる
- 青い部分 (1×2×・・・×(P-1))はつじつま合わせ
以上により小定理が証明されました。



コメント