こんにちは。Horyです。
これまでにファラデーの電磁誘導に関する様々な問題に取り組んできました。
今回の問題では、正方形コイルに関する問題に取り組みます。
非常に難しい問題ですが頑張りましょう。
問題 正方形コイル
以下に示すのはファラデーの電磁誘導の法則で正方形コイルに関する問題です。

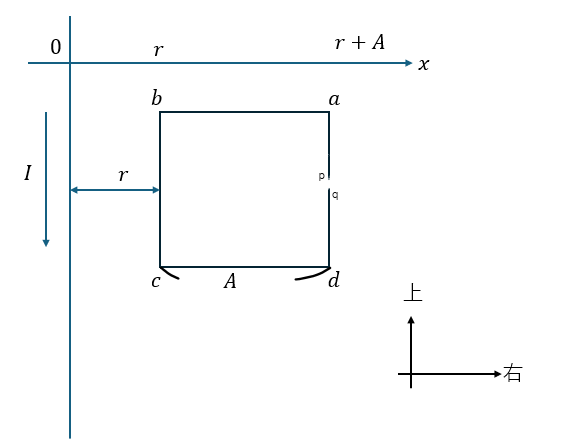
ここで、変位電流と定常電流に関してですが・・・
- 変位電流・・・時間によって大きさや向きが変化する電流
- 定常電流・・・時間によって大きさや向きが変化しない電流
(1)解答・解説
問題を解きます。まず、直線電流が作る磁束密度の向きや大きさは以下の記事にまとめたとおりなので証明はしません。
- 電流の時間変化
- 磁束密度の時間変化
- 磁束の変化を妨げる向きに誘導起電力が生じる
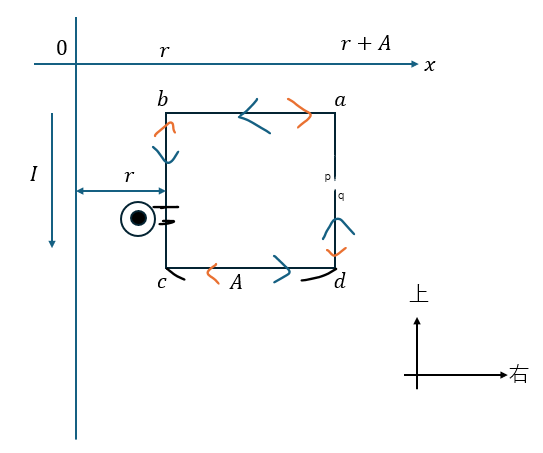
電流によってコイルにも磁束密度が誘起されます。そして、磁束密度の向きは導線を流れる電流について右ネジが回る向きです。
- 青い矢印・・・正方形コイルの正の向き
- オレンジの矢印・・・誘導起電力の向き

向きはオレンジの矢印の向きです。
フレミングの左手の法則で実践してみてください(レンツの法則を思い出すこと)。
ところで、p,qのどちらの電位が高いかについてですが・・・
「誘導起電力の向きは分かった。電流は電位の高い側から低い側に流れる。よってQの方の電位が高い」
上の考え方で合っているのでしょうか・・・結論から言うと考え方も答えも違います。
ここで、pq間を静電容量が非常に小さいコンデンサと考えてみます。
そして、回路の方程式を考えてみます。 誘導起電力は電位降下の和なのでPの方がQよりも電位が高いと言えます。コンデンサと考えたときにpに正電荷がたまって、qに負電荷がたまる
(2)解答・解説
この問題は、正方形コイルを上に動かす場合と右に動かす場合で個別に解説します。
どちらの問題も動かしたことで磁束密度がどうなるかを考えてみてください。
また、動かしていないときについても考えてみましょう。
正方形コイルを動かしていないとき
- 辺bc,ad・・・辺内で磁束密度変化しない(導線に流れる電流・導線からの距離が一定)
- 辺ba,cd・・・辺内で磁束密度変化 (電流が一定だが、距離が違う)
このことをよく考えてみます。
コイルを上(下)に動かす
コイルを上下に動かした場合を考えます。
コイルを上下に動かしても、導線からの距離が変化せず、電流も定常電流だから、誘起される磁束密度に変化が起こりません。
磁束密度に変化がないと言うことで誘導起電力は発生しません。だからp,qの電位は等電位になります。
コイルを右に動かす
仮にコイルを右向きに等速vで動かしたとしましょう。
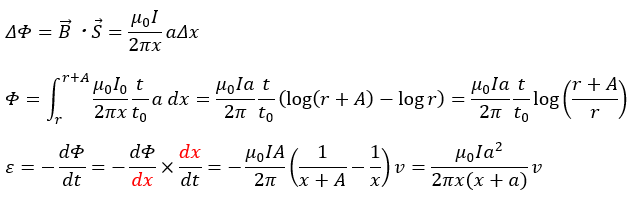
ここで、誘導起電力が発生するなら回路に電流が流れると言うことです。仮に、この回路の内部抵抗をRとして、流れる電流を求めてみましょう。
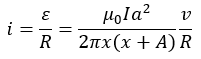
また、一定速度で運動すると言うことは、力が釣り合わないといけません。
どういうことかというと、辺baとdcにかかるローレンツ力は対辺で相殺しますが、辺adとbcについてはそうはいきません。
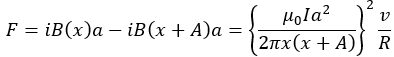
もちろん、この力の向きは右向き(b→a)になります。



コメント