こんにちは。Horyです。
前回の記事では、平行導体レールを一定の速度で動く導体棒に関する問題に取り組みました。
今回の問題は斜面を滑る導体棒に関する問題です。この問題では導体棒は等速で運動しません。加速しながら運動することになります。
今回も頑張りましょう。
問題 斜面を滑る導体棒
以下に示すのは斜面を滑る導体棒に関する誘導起電力の問題です。

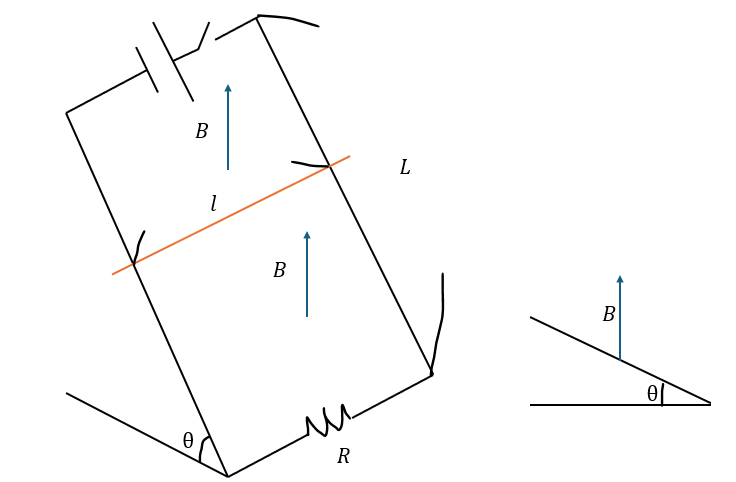
この問題を例に解説します。前回の問題よりも難しいですが頑張りましょう。
今回は導体棒に内部抵抗はありません。電池の方に内部抵抗があります。なので、導体棒間での電位降下は0になります。
(1)解答・解説 準備
(1)の解答・解説と共に、(2)の準備を行います。
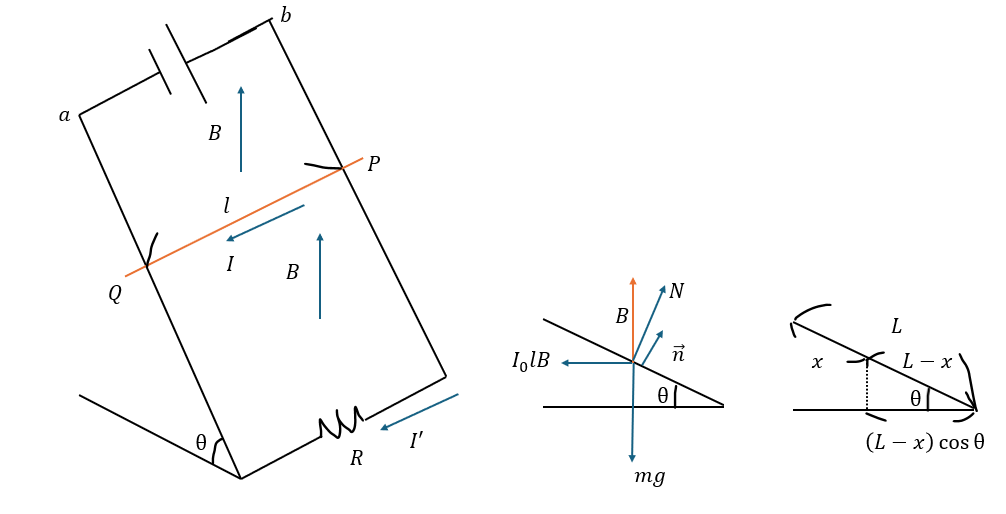
ここで、導体棒は導線と同じです。だから、導体棒間での電位降下は0になります。
なので、抵抗を流れる電流I’の値も0になります。
導体棒が動かないということは、斜面方向の成分が釣り合っていると言うことです。
導体棒に働く力を考えると・・・
- 重力の斜面成分の力 (力学的な力)
- 導体棒を流れる電流(電荷)が受けるローレンツ力の斜面成分の力(電磁気学的な力)
この2つの釣り合いの力を求めて導体棒を流れる電流をまずは求めます。
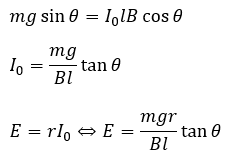
ここで、(2)のための準備を行います。導体棒が斜面を滑る時を考えます。
- 導体棒に誘導起電力が発生・・・速度が変化している→誘導起電力自体も変化
- 導体棒に電流が流れる・・・磁場より変化する力を受ける→電流も変化する
また、閉回路を以下のように設定します。
- 導体棒の下側の閉回路・・・C1
- 導体棒の上側の閉回路・・・C2
(2)解答・解説
運動の様子を説明すれば良いので、最終的には、物体の位置座標を時刻で表せれば良いです。

誘導起電力が2つあって厄介と思うかもしれませんが、安心してください。スイッチは切られています。だから、下側の回路だけ考えれば良いです。
電流の流れる向きやローレンツ力はレンツの法則より、下側の回路の面積が減少することで磁束の減少を妨げる向きに働きます。
- 導体棒に流れる電流の向き・・・P→Q
- ローレンツ力の向き・・・Q→a
この問題の手順です。
- 閉回路C2に流れる電流を求める
- 運動方程式で時間追跡
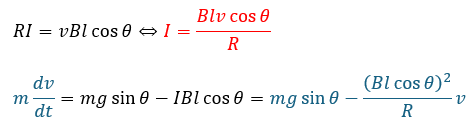
上の2つの式を言葉で説明します。
- 赤い式・・・vが大きくなると誘導起電力も増加→電流も増加する
- 青い式・・・赤い式から、棒の運動を妨げるローレンツ力の大きさも増加する
微分方程式を解く気はありませんが、空気抵抗型の微分方程式と全く同じです。終端速度を求めてみます。

最終的には等速運動と同じになります。そして、流れる電流も一定になって、重力の斜面方向の成分とローレンツ力が釣り合うことが分かります。
(3) 解答・解説
導体棒に起電力が発生しているので、導体棒を電池と見て、電池のする仕事を求めてみましょう。
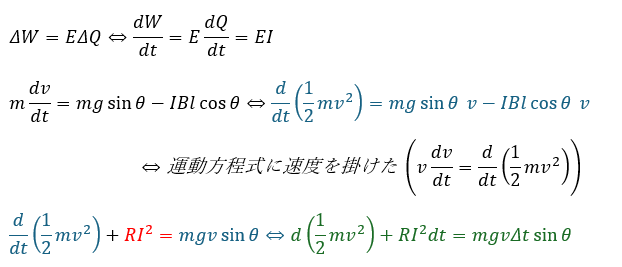
上の式は誘導起電力の仕事率の両辺を足したモノです。
- 緑の式の第1項・・・導体棒の運動エネルギーの変化
- 緑の式の第2項・・・抵抗で生じたジュール熱
- 緑の式の第3項・・・重力のした仕事
最終的には、速度が終端速度になって、一定となるので、運動エネルギーの変化は0になります。
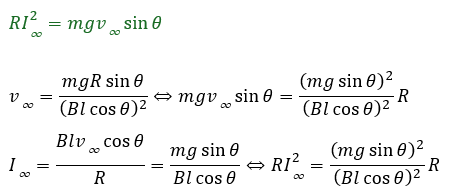
このようにエネルギー的な側面を考えると・・・電磁誘導は力学的仕事・エネルギーを電気エネルギーに変えるといっても差し支えないですね。



コメント