こんにちは。Horyです。
前回の記事で平行レール上を動く導体棒についての問題を2つ取り組みました。
今回の記事では回転する導体棒についての問題に取り組みます。
これも重要な問題になるので頑張りましょう。
円運動をする導体棒
以下に示すのは円運動をする導体棒に関する問題です。

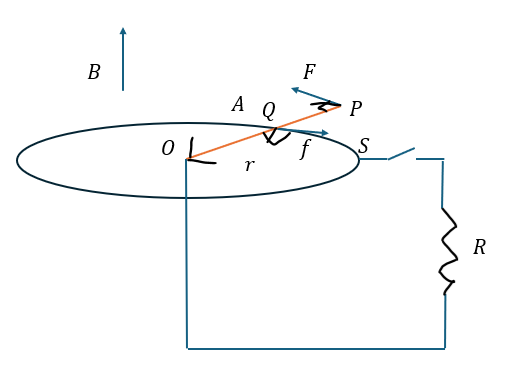
この問題を例に解説します。頑張りましょう。
(1)事前準備
この回路を上から俯瞰してみます。
回路を貫く磁束は変化しないので、紫の斜線部の磁束変化は無視します。
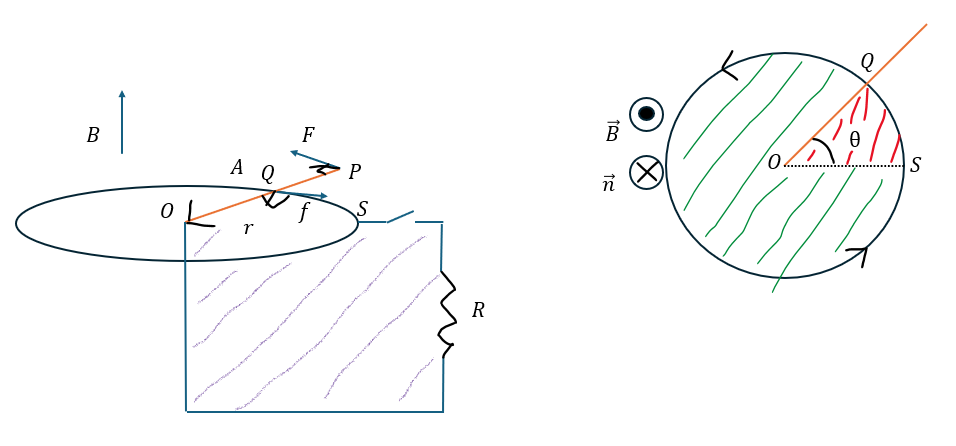
今回の問題では、磁束密度の向きと反対の方向に単位ベクトルを取ります。
磁束の変化は赤い斜線部と緑の斜線部のどちらでとっても構いません。
- 赤い斜線部・・・時間と共に面積が増える=磁束が増える
- 緑の斜線部・・・時間と共に面積が減る=磁束が減る
赤い斜線部でも緑の斜線部でもどちらを取っても同じ答えが出ます。
レンツの法則で磁束の変化を妨げる向きに誘導起電力が発生します。
(1)解答・解説

誘導起電力の向きはO→Qの向きです。
(2)解答・解説
まずは、電流の向きを考えると共に等価回路を示します。
本来、導体のため、抵抗は無視できるほど小さいですが、仮に抵抗を仮定するとして、キルヒホッフの法則を使って求めていきます。
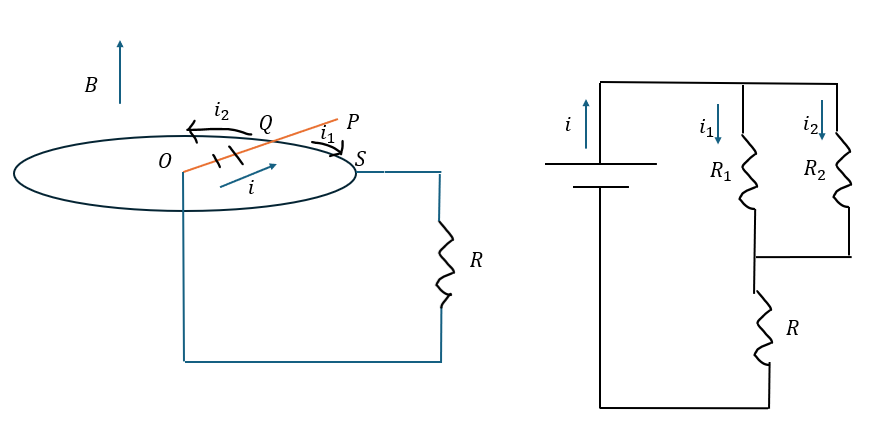
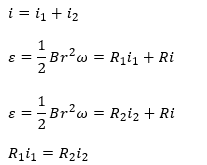
まぁ、復習も兼ねて自分でやってみてください。
(3)/(4)解答・解説
導体の抵抗は0と近似できるので、R1とR2は0に近似できます。
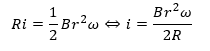
ここで、スイッチを入れているときと入れていないときの違いですが・・・
- スイッチを入れていない・・・断線している (電流流れない)
- スイッチを入れる・・・閉回路 (電流流れる→ローレンツ力)
つまり、誘導起電力が発生しても、回路として断線していれば電流は流れないと言うことです。
OQ間に流れる電流は磁束密度から導体棒の回転を妨げる向きにローレンツ力を受けるので、ローレンツ力に逆らって同じ角速度で回転させるには新たに力を加え入れる必要があります。
これが(4)の答えです。
加え入れる力をΔFとし、これについて考えてみましょう。
- riB・・・導体棒を流れる電流の受けるローレンツ力
- f・・・導体棒が受ける摩擦力
- F+ΔF・・・導体棒の端点に与える力
これは力のモーメントで考えるのが楽です。
一定の角速度ωで運動しているので、モーメントの釣り合いが成立します。
また、ローレンツ力は導体棒全体が受ける力とも言えるので、作用点は導体棒の中点と見なせます。

加え入れる力について、求めることができました。
エネルギーについて・・・
ちょっと発展的な内容になりますが、回転エネルギーという側面からも考えてみましょう。
回転において、仕事と仕事率は以下のように定義できます。
- 仕事=力のモーメントと回転角の積
- 仕事率=力のモーメントと角速度の積
運動エネルギーの変化分ΔKを考えてみます




コメント