こんにちは。Horyです。
前回の記事ではファラデーの電磁誘導の法則について原理から解説しました。
その中で問題に2つのタイプがあると説明して・・・
- type1;面積が変化することで磁束が変化する
- type2;磁束密度が変化することで磁束が変化する
また、発生する誘導起電力の向きが磁束の変化を妨げる向きに働くレンツの法則に関しても解説しました。
今回はこれらを応用してtype1の基本問題を解説します。
今回も頑張りましょう。
問題 回路を動く導体棒
以下に示すのは回路を動く導体棒の問題です。

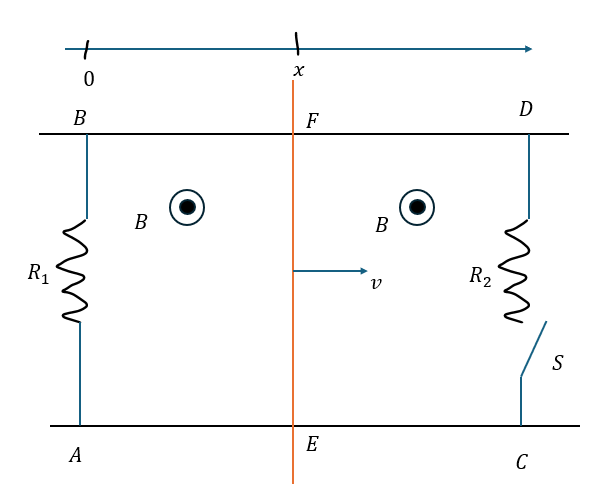
この問題を例に解説します。手順は前にも説明したとおりですが・・・
- ①;閉回路の生の向きを約束する(任意の向きで良い)
- ②;①の正の向きに右ネジを回してネジの進む向きに閉回路の囲む面の法線と単位ベクトルを取る
- ③;閉回路の囲む面積をSとして貫く磁束を考える
- ④;時速が変化すると回路に起電力が生じる(磁束を時刻で微分する)
また、磁束密度は回路を上から俯瞰してみたとき、こちらに向かう向きでアルコとは注意しましょう。
前半部分;問題を解く前の下準備
手順通りに問題を解いていきます・・・
- ①「A→E→F→B→A」の向きを正
- ②磁束密度の進む方向に単位ベクトルn
- ③ 囲む面積を求める
- ④ファラデーの法則に適用
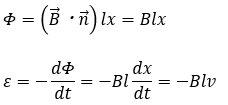
ここで、v>0なので、xの値は時間と共に、増えます。誘導起電力は磁束の変化を妨げる向きに流れるので、A→B→Fの向きに流れます。
また、εについて、今回は誘電率でなく、誘導起電力です。
前半部分 解答
前半部分の解答です。
事前準備の段階で誘導起電力は求めたので(1)については解決しています。
キルヒホッフの法則で電位降下の和が誘導起電力になることを利用します。
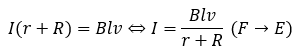
一応、余談ですが、電磁誘導によって流れる電流も磁束密度を作りますが、基本的にこの磁束密度B’は問題の磁束密度Bよりもはるかに小さく無視します。
これは暗黙の了解として覚えておいてください(無視できないときは問題文に指示があります)。
後半部分 問題を解く前の下準備
後半部分の問題を解く前の下準備です。
左側の海路については前半部分の準備で解説したので、右側の回路を考えます。
- ①「D→F→E→C→D」の向きを正
- ②磁束密度の進む方向に単位ベクトルn
- ③ 囲む面積を求める
- ④ファラデーの法則に適用
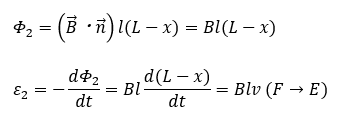
後半部分 解答・解説
左側の回路と右側の回路で分けてファラデーの電磁誘導の法則を用います。
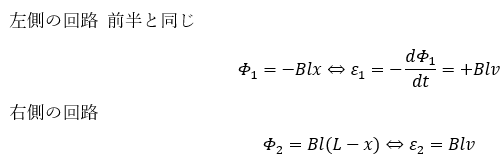
ここで、キルヒホッフの法則についておさらいします。
- 分岐点での電流の流入量と流出量は等しい
- 電位降下の和が起電力になる
今回は右側と左側で閉回路ができているので、キルヒホッフの法則を適用します。
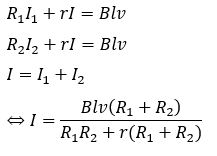



コメント