こんにちは。Horyです。
前回の記事ではドップラー効果について現象の理解と原理を解説しました。
今回の記事ではドップラー効果の問題をいくつかまとめようと思います。
今回の記事では3つのテーマに関して取り組もうと思います。
- 近似式を用いるドップラー効果
- 風や反射板がある状態でのドップラー効果
- 円形コースのドップラー効果
これらの3つの問題について取り組もうと思います。これらが理解できればドップラー効果に関しては怖いものなしかと思います。
近似式を用いるドップラー効果
以下に示すのは近似式を用いるドップラー効果に関する問題です。

この問題を例に解説します。頑張りましょう。
問題を解く前の事前準備
まずは、問題を解く前の下準備です。
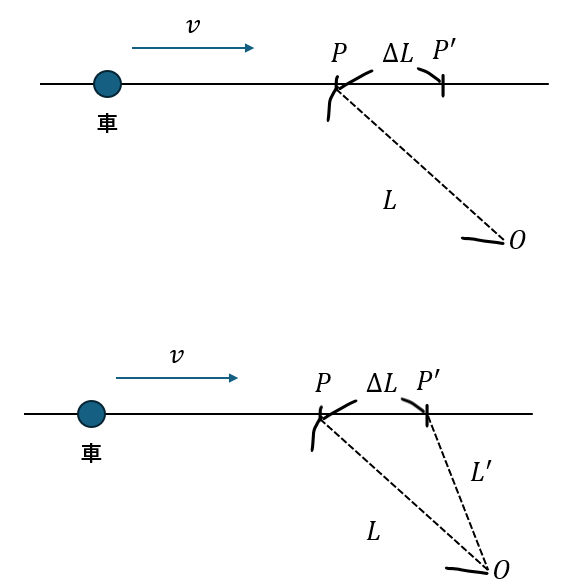
当たり前ですが、音源速度(車)によらずに音波は発した点から空気に関して音速Cで伝わります。
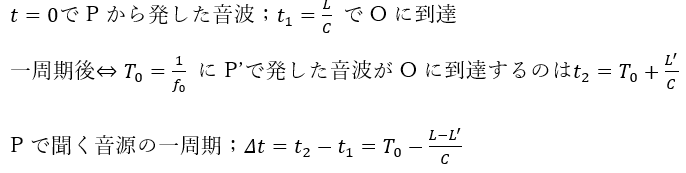
ところで、問題文にはL’が存在しませんので、何とか出してくる必要があります。
OPP’で三角形ができていますねぇ。余弦定理を用いましょう。
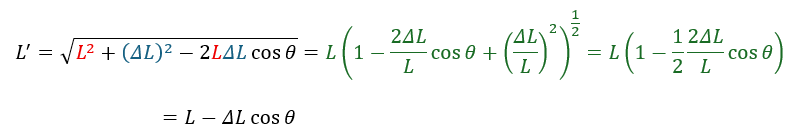
上の式の緑の部分に関しては近似式を用いました。
解答・解説
問題の解答・解説です。
Pから出た音波は一周期後にP’に到達するので、ΔLは以下のように書けます。
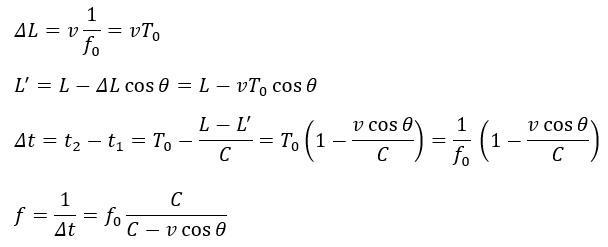
上の近似式の処理は電磁気などの様々な物理の分野で出てくるので絶対に覚えておいてください。
風や反射板がある状態
風や反射板がある状態でのドップラー効果の問題です。

この問題を例に解説します。頑張りましょう。
(1)解答・解説
まぁ、この(1)に関しては前回の記事でもやったのでできてほしいです。
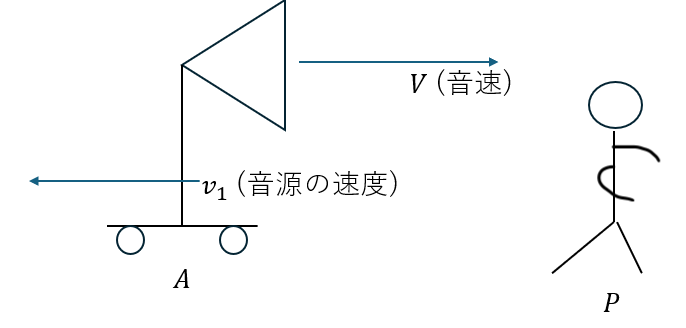
音波の進む速さが音源の動きに無関係です。波源が動くので波長が変わります。
まずは、波源から見た音波の波長を求めます。次に振動数を求めます。
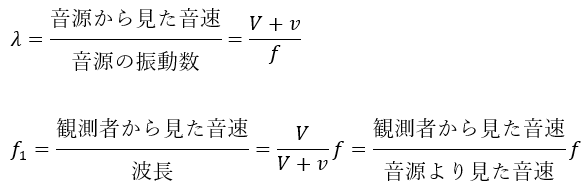
基本的に前回の記事のパターン③で出てきた公式通りです。
(2)解答・解説
速度を全て「空気に対しての速度」と考えれば無風のときと同じです。
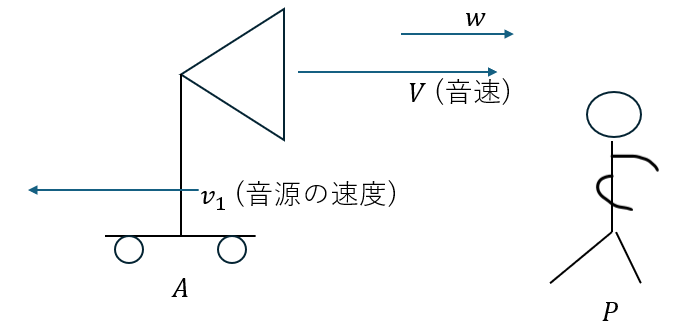
または、Vが空気に関しての音速なので、これを「地面についての音速」に置き換えてもOKです。

(3)解答・解説
図にしてみます。反射板が一定速度で動きます。
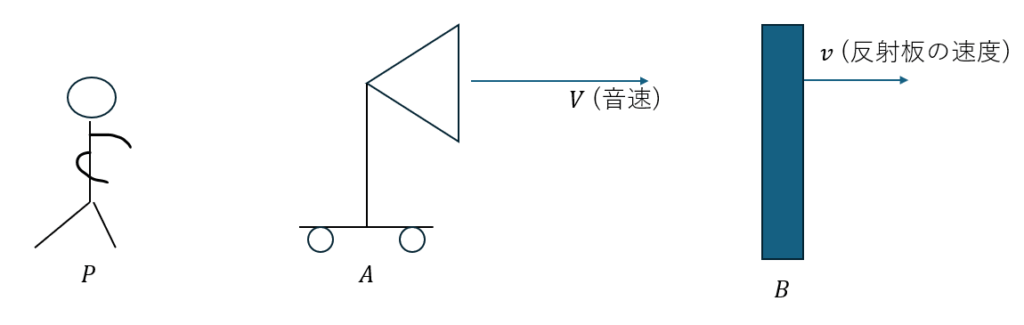

反射板は上に示す振動数の音源を反射音として出します。反射板を音源とみなします。

うなりに関しては自分でやってみてください。
円形コースのドップラー効果
円形コースのドップラー効果の問題です。これも応用問題として頻出します。

この問題を例に解説します。頑張りましょう。
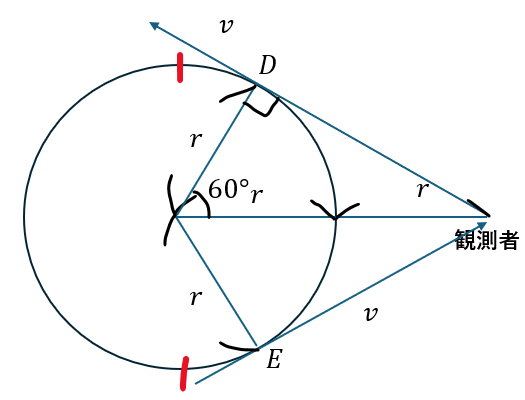
解答・解説
解答・解説です。よく勘違いする人の特徴として、車が赤線部の時が振動数最大・最小という人がいますが間違いです。
- 振動数の最大値・・・音波が観測者に対して直線的に近づく (点E)
- 振動数の最小値・・・音波が観測者に対して直線的に遠ざかる (点D)
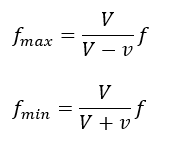


コメント