こんにちは。horyです。
前回の記事ではデータにおける代表値として平均値・中央値・最頻値に関して解説しました。
上の記事でも挙げていますが、平均値の罠に関する問題はかなり大事なので覚えておいてください。
今回の記事では四分位数と箱ひげ図に関して解説します。
今回も頑張りましょう。
四分位数について
四分位数とは簡単に説明するとデータを4つに分けるための仕切りのことです。
4つに分けるためには仕切りは3つあれば良いので四分位数は3つあります。
(当然ですが、データが4つ以上ないと四分位数は定義できません)
- 第2四分位数・・・中央値
- 第1四分位数・・・最小値から第2四分位数でデータを見たときの中央値
- 第3四分位数・・・第2四分位数から最大値でデータを見たときの中央値
ここで、四分位数を文字で以下のように定義します。

n個のデータを左から小さい順に以下のように並べることとします。

- 範囲・・・全てのデータが含まれる幅
- 四分位変位・・・データのほぼ半分が含まれる幅
- 四分位数でデータをほぼ4分割することが可能
ここで、中央値はデータの数が偶数の時と奇数の時で処理が違うことを前回の記事で解説しました。
四分位数も中央値が関わっているという時点でデータ数によって処理が違うことになります。
データを4つに分割しているということで、4の倍数が絡みそうですね。
データ数が4の倍数

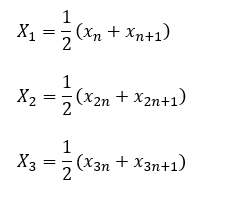
データ数が4で割って1余る

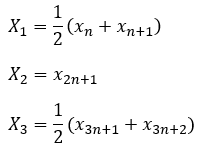
データ数が4で割って2余る

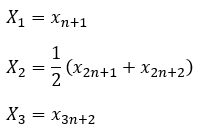
データ数が4で割って3余る

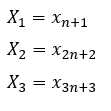
箱ひげ図の作り方
箱ひげ図の作り方を簡単に解説します。
作成に必要な要素は5つあります。
- 最小値
- 最大値
- 第1四分位数
- 第2四分位数(中央値)
- 第3四分位数
用いるデータは前回使用したボール投げの飛距離のデータです。
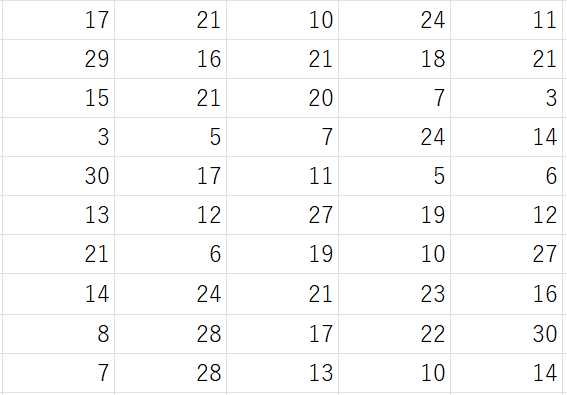
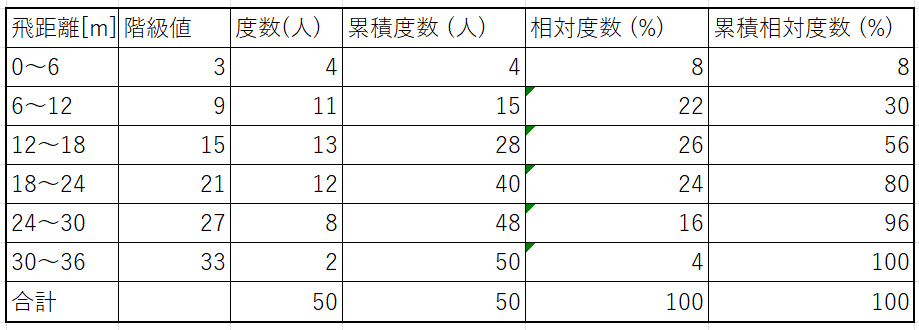
データ数が50個あるので、四分位数はデータが4で割って2余る場合に従いします。
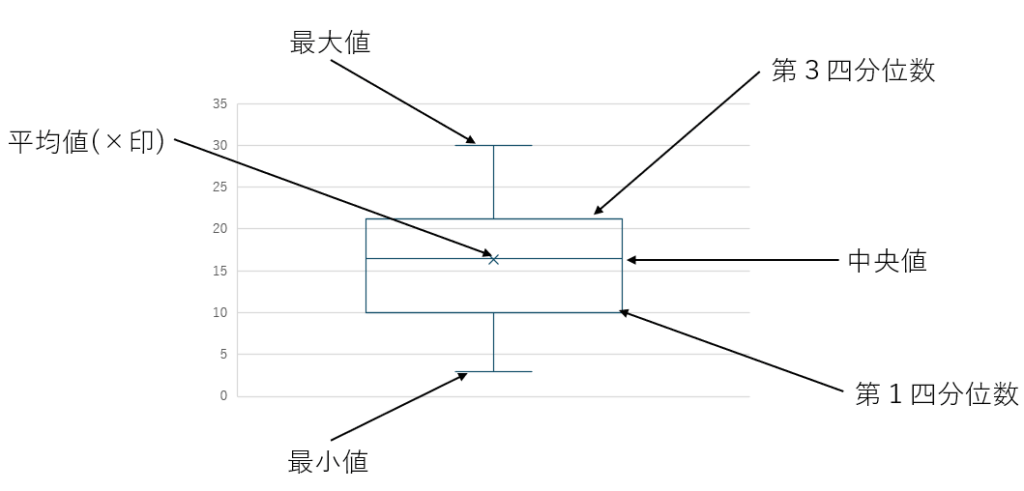
エクセルの仕様上、飛距離の軸が縦軸になっていますが、試験では横軸になっています。
ただ、縦でも横でも言っていることは同じです。
箱ひげ図の作成手順は以下の通りです。
- ①;第1と第3四分位数を向かい合う辺とした長方形を作る (箱の部分)
- ②;①で作った箱の中に中央値に対応する線を引く
- ③;最大値と最小値の線を引く
- ④;最小値から第1四分位数まで線を引く (ひげの部分)
- ⑤;最大値から第3四分位数まで線を引く (ひげの部分)
以上の5ステップで箱ひげ図は完成します。
平均値を書き入れるかどうかは自由ですが、書き入れるのであれば対応する場所にバツ印とかを書けばいいと思います。



コメント