こんにちは。Horyです。
これまでにヒストグラムや代表値、箱ひげ図などについて解説してきました。
今回の記事では多くの学生を悩ませている分散と標準偏差の意味を解説するとともに、分散を計算で早く求めるテクニックも解説していこうと思います。
今回も頑張りましょう。
分散と標準偏差
データ数はn個あるとして以下のように定義します。
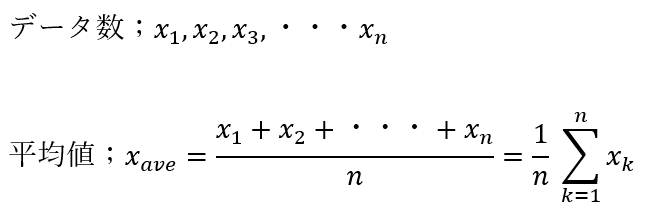
分散と標準偏差は以下のように表せます。
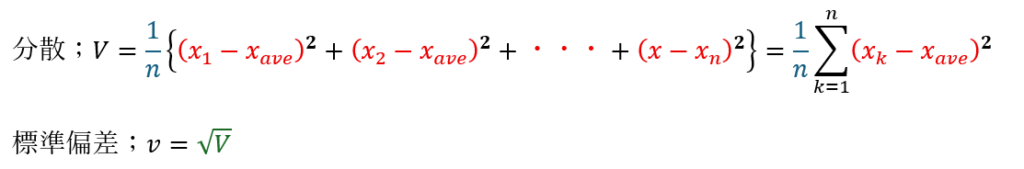
式だけを書いても読んでいる人は「どういうこと?」って思うので解説します。
- 赤文字の部分(偏差)・・・各データが平均値からどの程度離れているの?
- 二乗する意味・・・平均値からの距離を一辺とした正方形の面積
- 青文字の意味・・・データ数で割っている→平均化
- 分散の意味・・・データのばらつきを面積で表している
- 緑の部分・・・分散の平方根をとっている
- 標準偏差の意味・・・平均値からのばらつきを定量的に評価 (偏差の標準化)
分散や標準偏差がデータの「ばらつき」を表すと解説しましたが、「データが平均値からどの程度の広がりを持っているの?」という意味でのバラツキです。
ここまで説明して何とか分散と標準偏差の意味が分かったような気もしますが、いくつか疑問もあると思いますので解説します。
疑問1;分散だけでも良いのでは?
分散・標準偏差のどちらもデータが平均値からどの程度離れているか(どの程度ばらついているか)を表す量です。
どちらも、バラツキを表す量なら別に分散だけでもよくて標準偏差なんていらなくね?って思います。
標準偏差という概念がある理由は単位にあります。
先ほどの説明で分散が「各データの平均値からの距離を一辺とした正方形の面積の平均化」という話はしました。
ということは、面積である以上、分散の単位は元のデータの単位の二乗になります(例えば、データの単位が[m]ならば、分散の単位は[m^2]になる)。
統計はデータの比較を行うことがよくあるので、単位を元のデータと合わせた方がいいと考えて、分散の平方根をとって標準偏差としました。
これにより、「標準偏差が~[m]だから、このデータは平均値から~[m]の広がりを持つ」という表現ができるようになりました。
分散では上のように言うことはできません。単位が元のデータと分散で違うからです。
疑問2;絶対値で評価できないの?
どういうことかというと・・・分散と標準偏差は以下のように求めれましたが・・・
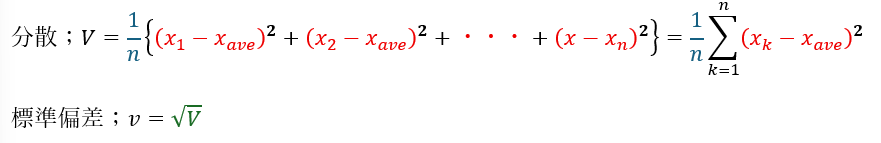
次の式に示すようにバラツキを評価してもいいんじゃないのか、、、と思います。
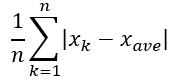
上に示すように各データと平均値の距離(絶対値)の平均を求めるやり方です。
このように「絶対偏差」を用いてデータのバラつきを評価することも可能です。
分散・標準偏差の計算
分散や標準偏差を求めることはデータが多ければ多いほど面倒です。
例えば以下に示すように5つのデータがあったとしましょう。
- 5, 6, 10, 6, 2
普通にやると以下のように求めれます。
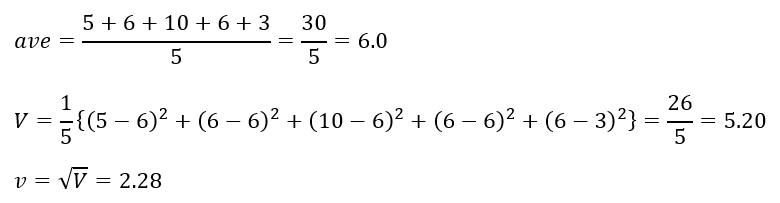
このように求めると非常にめんどいです。
ちなみにですが、偏差・分散・標準偏差は元の桁数より2桁多く導出するのがルールです(今回なら生データは整数なので、分散と標準偏差は少数第二位まで求める)。
簡単に求める方法を以下に紹介します。
まずは、分散の定義を書き下します。
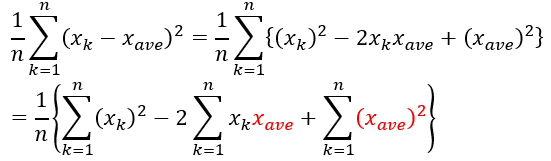
ここで、赤い部分はkに関係しない定数になりますのでΣの外に出せます。
「どういうこと?」と思うかもしれませんが、平均値の意味をよく考えてほしいです。

これって、kに依存しないので絶対に変わりませんよね、、、(そもそも、平均値は全データの和をデータ数で割ったものなので変わりようがない)
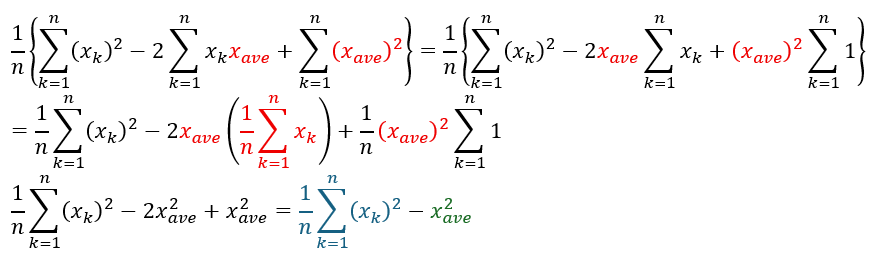
- 青い部分・・・二乗の平均値
- 緑の部分・・・平均値の二乗
- 分散;二乗の平均値から平均値の二乗を引いた量
Σの基本性質に関してはこちらの記事に解説してあるので見といてください。
これは覚えておく価値がある式です。実際にやってみると・・・
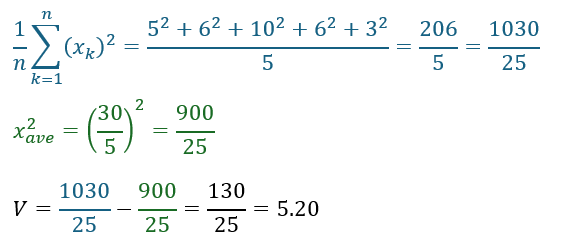
このように分散を比較的簡単に求めることができました。
二つのデータが関数の関係に
二つのデータが関数の関係になっている場合を考えます。
データをy,zとして、両者に以下に示す関係があるとします(ただし、a,bは定数とする)。
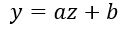
以下の3つの式が成立します(ただし、Vは分散とします)。
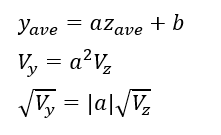
証明していきます。
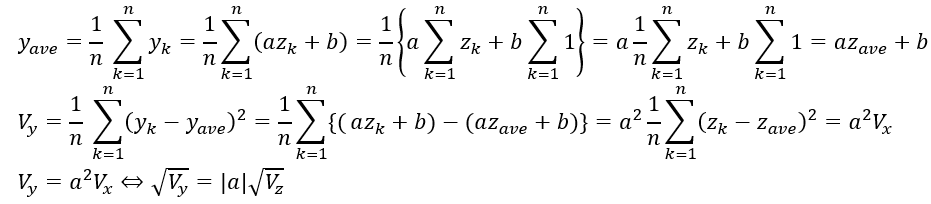
以上によって証明が完了しました。
応用;変動係数
分散や標準偏差の応用として変動係数があります。
どういうことかというと、測定しているスケールの異なるデータや単位が異なるデータがあった時を考えます。
- 例1;長さに関するデータ
- 自動車100両の移動距離のデータ
- 100人の身長のデータ
- 例2;単位が異なるデータ
- 100人の睡眠時間のデータ
- 100人の体重のデータ
例1と例2共に、テーマが異なるデータであるため平均値を始めとした代表値を比較することは当然できないです。
しかし、平均値からのバラつきは比較ができます。ただし、標準偏差で比較することはできないです。
何でかっていうと・・・
例1は長さ(距離)であることに違いはありませんが、スケールが全く違います。
自動車なら移動距離が数千~数万 kmなので、標準偏差の単位は km
身長なら1~2mなので標準偏差の単位は m
例2は単位がそもそも違います。
睡眠時間なら標準偏差の単位は時間
体重なら標準偏差の単位は kg
そんな時に使えるのが変動係数です。以下のように定義されています。
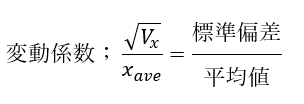
Vが分散です(分散の平方根が標準偏差)。
標準偏差を平均値で割った値が変動係数で単位はありません(無次元の量)。
変動係数であればあらゆるデータにおける平均値からのバラつきの程度は比較できます。

コメント