こんにちは。Horyです。
今回の記事では数学のデータの分析とヒストグラムの作り方に関してまとめようと思います。
データの分析は共通テストにしか出ないため、対策や勉強をしている人が少ないように感じます。
(共通テストにしか出ない・・・は言い過ぎかもしれないが、少なくとも、二次試験の問題でデータの分析の問題をほぼ見たことがない)
ただ、私はこの分野が数学の中で最も社会に応用が効く分野だと考えているのでそういった点も含めながら解説します。
今回も頑張りましょう。
データの分析を学ぶ前に・・・
データの分析について学ぶ前に話しておかなければならないことがあります。
そもそも、この分野が何で共通テストだけにしか出ないかを考えたことはありませんか?
ここからはあくまでも私の考察ですが、、、
データの分析が共通テストにしか出ない理由は「数学の1つの分野であることは間違いありませんが、他の数学分野とは一線を画するから」じゃないのかなと思います。
というのも、この分野は厳密に言うと「統計学」という分野になります。
実際に、共通テストでも、数学ⅠAの「データの分析」や数ⅡBの「確率密度関数」に関しては「作問責任者が共通テスト問題政策委員会とは異なっている」という話を聞いたことがあります。
(どこだったかは正確に覚えていませんが、確か日本統計学会だったような気がする)。
つまり、問題の責任者が「数学のプロ」ではなく「統計のプロ」ということがポイントです。
そのため、数学の他の分野とは攻略の方法などが違うということを頭に入れておかなければなりません。
(そういう私も統計のプロではないので攻略法とかはあまり知りません。ただ、この分野は考え方とかが少し違うということは意識しないといけないです。)
また、私のブログではあくまでも「高等数学の教科書」に書いてある表記方法に従うと言うことも言っておきます(統計学の専門書とは違う部分があると言うこと!)
データとは何か・・・
皆さんは身体測定の時間にボール投げとかをしたと思います。
ボール投げとはボールを投げて飛んだ飛距離を記録する一連の作業のことです。
- ボール投げという行為・・・測定
- 飛距離を記録する・・・測定を記録する
- ボールが「何m」飛んだ?・・・変量
- 変量を要素としてまとめたもの(まぁ、大抵はたくさんの変量をまとめる)・・・データ
- 変量・・・「測定値を数値で表したモノ (特性を数値で表す)」
- データ・・・変量の集合
とはいっても、映像やアンケートの回答も自然科学の世界ではデータと言えるので「測定値を数値で表した変量をまとめたモノだけがデータである」というのは間違っているような気もしますが、一旦、置いておきます。
これらについては頭に入れておいてください。
ヒストグラムを作る
データを用いてヒストグラムを作ってみます。
以下はヒストグラムに用いる50人のボール投げの記録になります。
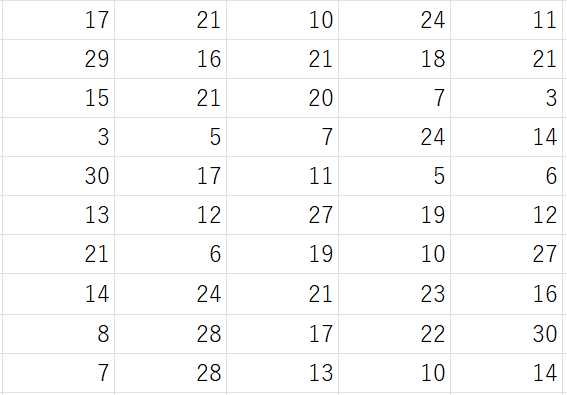
表にまとめます。
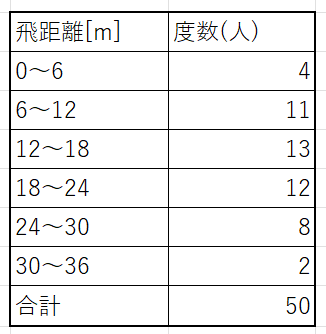
表の「0~6」の意味は「飛距離が0 m以上で6 m未満」という意味です。
- 表・・・度数分布表
- 表での変量区間・・・階級 (今回なら0 m以上、6 m 未満)
- 区間の中央・・・階級値 (0 m以上、6 m 未満なら階級値は3 m)
- 各階級でのデータの個数・・・度数 (0 m以上、6 m 未満なら度数は4)
- 各階級での度数が合計に対してどの程度を占めるか・・・相対度数
- (0 m以上、6 m 未満なら相対度数は4÷50≃8.0[%])
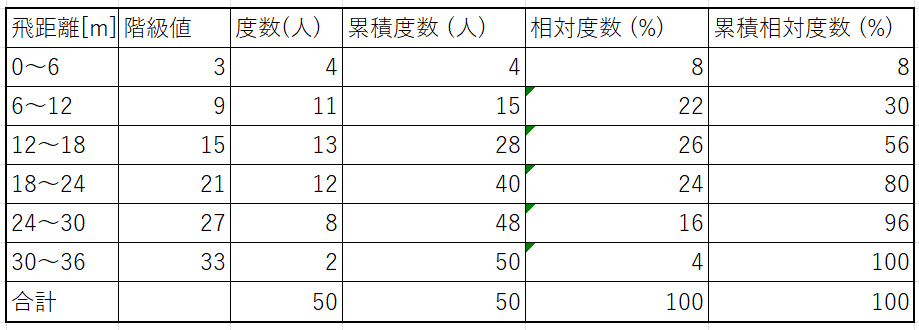
- 度数の合計・・・累積度数
- 相対度数の合計・・・累積相対度数
ここまでの知識を問う問題は共通テストでは出たことがないので覚えなくても良いです。
ただ、知識として知っておいてください。
以上のデータをヒストグラムにしてみます。
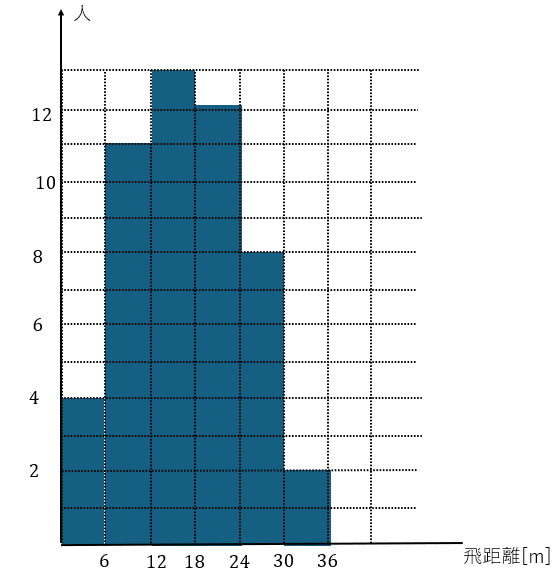
ヒストグラムの長所は階級の幅を適切に設定すればデータのバラツキを初めとした傾向が一目瞭然であることです。
階級の幅の適切な設定方法も統計学上のルールがありますが、共通テストで聞かれることはなく、グラフを記述する問題も出ないので安心してください。
ただ、グラフがどんな風になるかは頭に入れておいた方が良いです。
共通テストではグラフからどういったことが言えるかを選択形式で問わせる問題が非常に多いです。
これらに解答できるようになるためには代表値の意味を理解しないといけないので次回は代表値に関する記事を書きます。


コメント