こんにちは。Horyです。
皆さんはチェビシェフの多項式というのを知っていますでしょうか？
高校数学の教科書には出てこない内容ですが非常に面白いので今回の記事ではチェビシェフの多項式に関する問題を解説します。
今回も頑張りましょう。
問題；チェビシェフの多項式
以下に示すのはこの記事で取り組む問題です。
この問題を例に解説します。
2つの方法があります。
- 方程式に代入する方法
- 共有点条件
これらについて個別に解説します。
方程式に代入する方法
方程式に代入する方法です。
試行錯誤して3つの式を変形してみます。
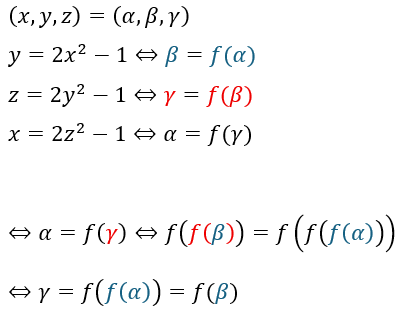
上の関係はかなり重要になってくるので覚えといてください。
実数解の範囲
連立方程式の解を(α,β,γ)としてみます。
ひとまず、y = f(x)のグラフを書いてみます。
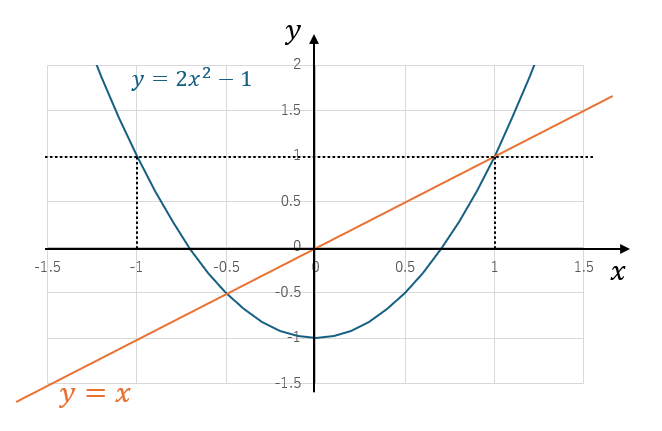
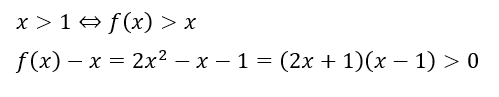
ここからは、背理法でα>1として矛盾を導きます。
背理法に関する記事はこちらです。
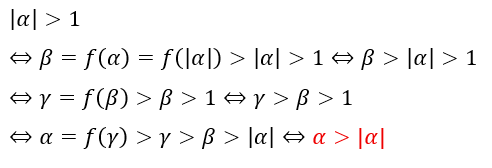
上に出る赤い式が矛盾します。α>|α|になることはあり得ません。
だから、実数解の範囲は|α|≦1です。
以上の事がβやγを起点としても起こるので|β|≦1, |γ|≦1です。
この条件(絶対値が1以下)から三角関数を導入することを思いつくことができるかどうかが鍵になります。
連立方程式をθで一変数化します。
実数解の個数
ここで、三角関数のcosθを導入します。
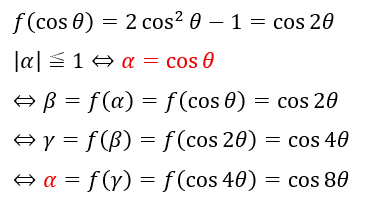
ここまで来たらcosθのみの方程式が出来ます。上の式の赤い部分に注目してください。
よって、この連立方程式は8個の異なる実数解を持ちます。
ところで、θの範囲が0≦θ≦πであることに疑問があると思います。
この理由は問題文に隠されています。「異なる」実数解の個数です。
もしも、0≦θ≦2πとかになると、同じになる解が出てくることになるからです(三角関数が一周すると元の場所に戻る)。
共有点条件
共有点条件を用いた解答方法です。
これはグラフを用いて解析的に解答する方法を紹介します。
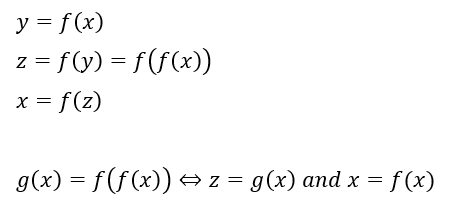
「z = g(x)」と「x = f(x)」の2つの関数を連立させてグラフ化します。
グラフ化したときの共有点の個数が異なる実数解の個数です。
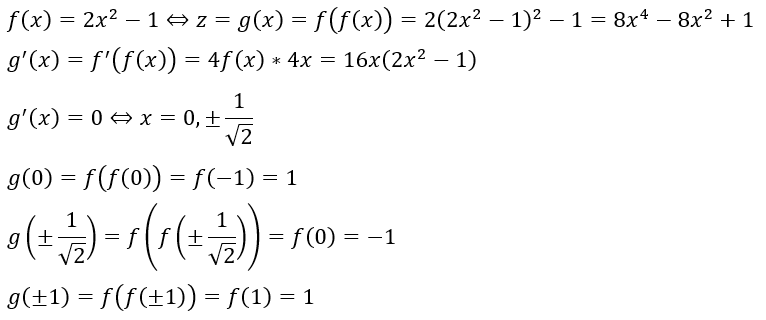
改めて、まとめると以下の2つをx-z平面にグラフ化すれば良いです。
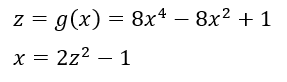
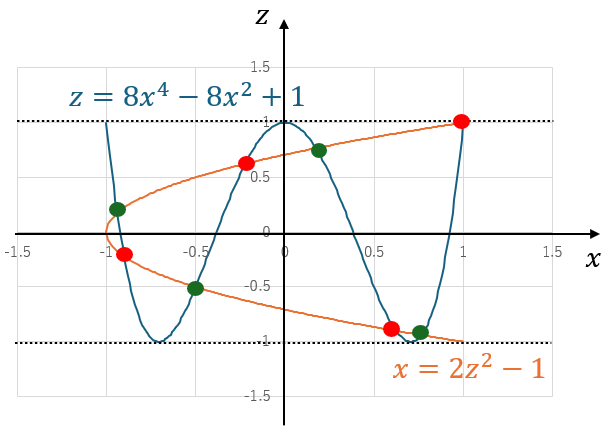
上の図から共有点の数は少なくとも8個存在します。
また、8次方程式の解なので、グラフに示す8個以外に解を持つことはありません。なので、解は全て実数で異なる8組です。
しかも、それらの解は全て－1～+1の範囲に入っています。
余談；チェビシェフの多項式について
チェビシェフの多項式について紹介します。
上の等式を満たす多項式Tn(x)ができて、これをn次のチェビシェフの多項式と呼びます。
何を言っているかというと、cos nθ は最小単位のcosθで表すことが出来て、これに付属する係数Tnをチェビシェフの多項式と言っています。
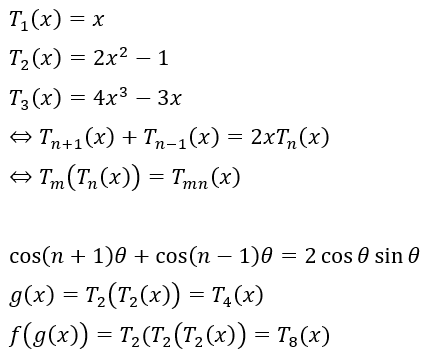
知識程度に知っておくと良いです。
