こんにちは。Horyです。
今回の記事ではストークスの定理を証明します。
ガウスの定理は、体積分と面積分を繋げる定理で、「立体の表面から出るベクトル量と立体の内部から湧き出るベクトル量は等しい」という定理です。
一方で、ストークスの定理は線積分と面積分を繋げる式で、物理では磁場と電流の関係を説明できます。
今回の記事ではこのストークスの定理について解説します。
今回も頑張りましょう。
ストークスの定理
ストークスの定理とは簡単には以下のような定理のことです。
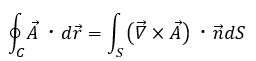
右辺と左辺の意味を解説します。
- 左辺・・・回転の接線方向の成分の和 (線積分)
- 右辺・・・微小面積dSについて、それぞれの加点の接線方向を取って足した。
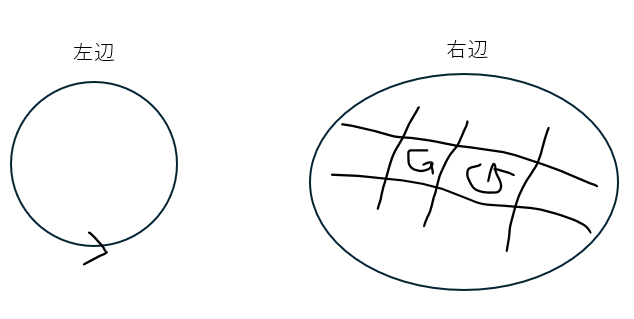
まぁ、ここまで言っても分からないと思うので証明していきます。
ストークスの定理 証明
ストークスの定理について、簡単な例を出して証明します。
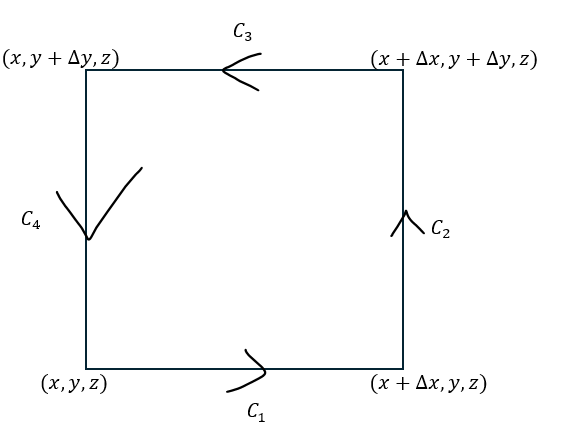
上の図で、任意のベクトルAをC1→C2→C3→C4の順に線積分するとします。
ストークスの定理の左辺を考えます。
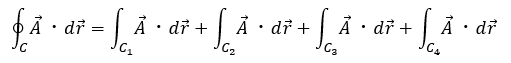
線積分や微分演算子について分からなければ、こちらの記事に戻ってください。
ここで、ベクトルAを座標で設定すると共に、線積分を考えます。

ルート1からルート4までを全て足し合わせます。
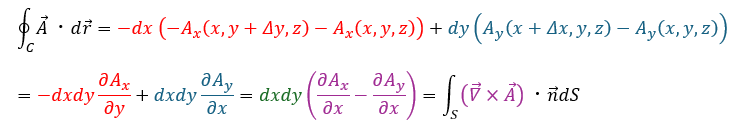
- 赤い部分・・・dyを∂yで相殺 (どちらも微少量∩同じ量)
- 青い部分・・・dxを∂xで相殺 (どちらも微少量∩同じ量)
- 緑の部分・・・この長方形の面積
確かにストークスの定理が成立していることが分かりました。次からはストークスの定理に関するちょっとした問題に移ります。
次回からはこれを用いてアンペールの法則を証明していきます。



コメント