オイラーの多面体定理の証明正多面体の個数

こんにちは。horyです。

前回の記事では平面グラフにおけるオイラーの公式を証明しました。

今回の記事ではオイラーの多面体定理の証明を前回の記事の内容を応用することで解説していきます。

今回も頑張りましょう。

多面体の定義

多面体定理に関して証明する前に多面体の定義を解説します。

多面体とは「複数の多角形で囲まれた空間図形」のことです。

この多面体の中で、多面体の表面or内部で任意に二点を取って、二点を結んだ線分がその多面体の内部 or 表面にあるものを凸多面体と呼びます。

凸多面体ではない図形はあるのか？と疑問に思うこともあるかもしれませんが普通にあります。

例えば、ポ○ケモンの「げんきのかたまり」みたいな形をした図形は凸多面体ではありません(とげとげの部分に二点を取ると線分が立体を突き抜けるから)。

凸多面体の中で全ての面が合同な正多角形で全ての頂点に集まる辺の数が等しい立体を正多面体と呼びます。

多面体の定義と種類は覚えておいてください。

オイラーの多面体定理とは凸多面体に成立する定理のことで以下の式が成立します。

上の式がオイラーの多面体定理の公式です。

公式の証明に前回の記事で示した平面グラフのオイラーの定理を利用します。

ここで、「平面グラフのオイラーの定理って二次元で成り立つ公式であって、３次元の立体図形と関係なくね？」って思う人もいると思います。

ちゃんと関係しているので以下で証明します。

多面体定理を証明します。

ここで、以下の図に示すような凸多面体を考えます。

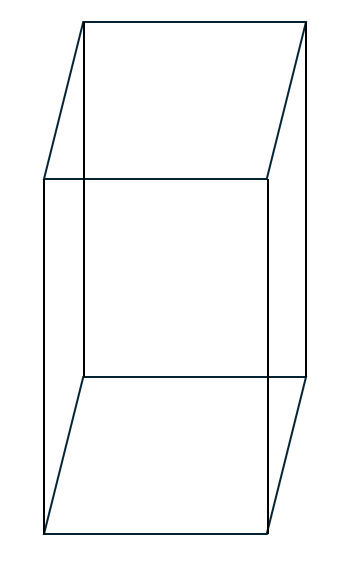
上に示すのは簡単な例として四角柱を示していますが、凸多面体であればなんでもいいです。

この凸多面体が伸縮性のあるゴムでできているとします。

凸多面体の任意の面を底面として底面を伸ばすことを考えます(上面が収まるように伸ばす)。

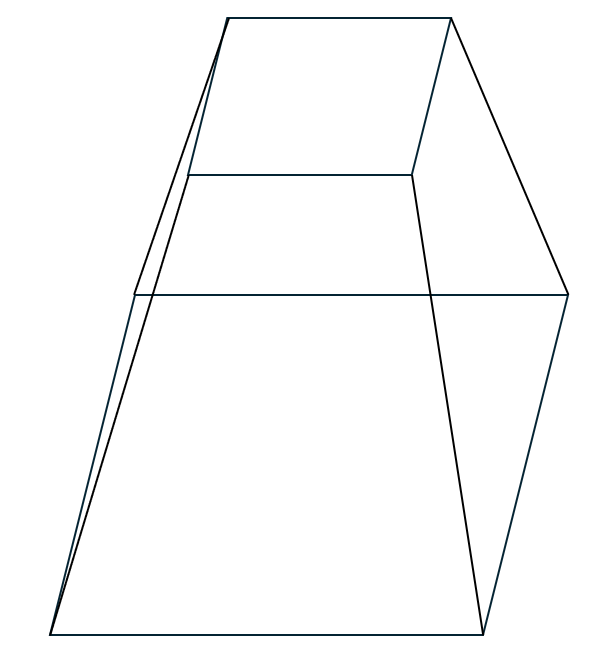
この図形を上面から見るとどんな図形になるか考えていただきたいです。

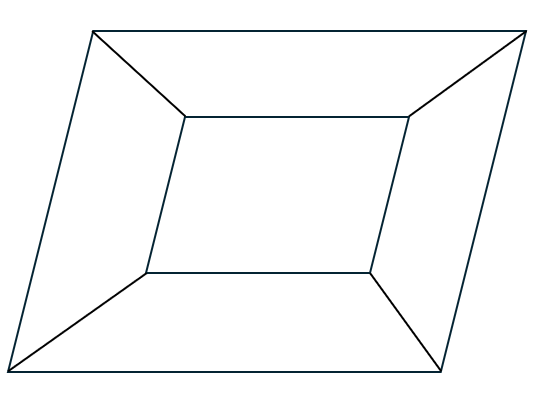
この上面から見た図形は連結な平面グラフです。

立体図形と平面グラフにおける図形の頂点・辺・面の数を考えていただきたいです。

四角柱を例に考えると・・・

立体図形を平面グラフで見たときに変わるのは面の数だけです。

高さがなくなって底面という概念がなくなるので面の数が一個だけ減ります(これは、全ての凸多面体で成立します)。

なので、立体図形時の頂点・辺・面の数をv,e,fと置くと平面グラフにした時にオイラーの公式が成立するので・・・

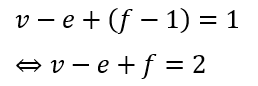
以上からオイラーの多面体定理は成立します。

正多面体の個数について解説します。

上の情報から正多面体の頂点・辺の個数は以下のように表せます。

何でこんな風に表せるかというと・・・

求めた値をオイラーの公式に代入します。

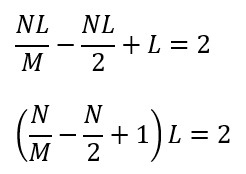
ここで、M,N,Lは３以上の整数になるので整数問題に帰着できます。

この形であれば整数問題の定石である「範囲の絞り込み」→「約数×約数」の形に持っていきます。

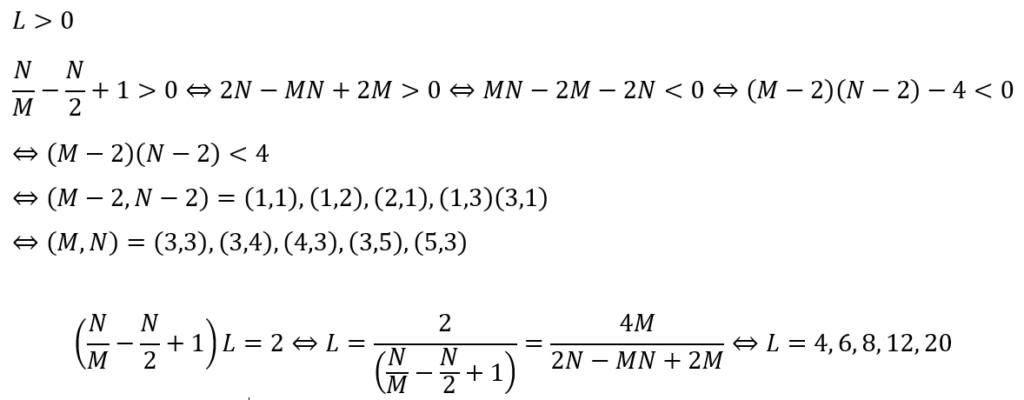
以上のことから正多面体は５種類しか存在しません。