こんにちは。Horyです。
これまでに数学Ⅲでは極限の定義や問題について解説しました。
高校数学では上のような方法で極限を定義しても差し支えないですが、大学の数学科では上のような方法で極限を定義することはしません。
大学の数学ではイプシロン-デルタ論法と呼ばれる方法を用いて極限を定義します。
イプシロン-デルタ論法は大学数学の最初の壁であり、多くの大学生が分からなくて悩んでいるという話を聞きます(実際に僕もよく相談された)。
今回の記事では高校数学での極限の定義の問題点を説明すると共に、その問題点を克服したイプシロン-デルタ論法を解説します。
今回も頑張りましょう。
高校数学の極限の定義の問題点
高校数学での極限は以下のように定義します。
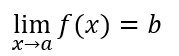
- 右辺の意味;関数f(x)のxをaに近づける
- 左辺の意味;bという値
- 式の意味;関数f(x)のxをaに近づけるとbに限りなく近い値になる
- 結論;f(a)=bである
上のように極限を定義して「何が問題なのか?」と思うかもしれませんが問題があります。
結論から言うと、「近づける」という表現に問題があります。
というのも、「近い」や「遠い」というのは程度の話で、人によって程度は違いますよね。
例えば、「xをaに近づける」といって、xをaから「1mm」の地点まで近づけたとします。
「1 mm」という距離は「宇宙物理を専攻している人」にとっては無視できるほど十分に小さい幅かもしれませんが、ナノ物理を始めとした「原子レベルの研究を先行している人」にとっては小さいとは言えない幅です。
「近いの程度」が人によって異なるので、xとaの幅をどれだけ小さくしても「いや、それは私にとっては小さくなくて無視できない幅でないから極限は定義できない!」と難癖をつける人が必ず出てきます。
これが高校数学での極限の問題点です。
イプシロン-デルタ論法
上に示した問題点を克服したのがイプシロン-デルタ論法です。
ギリシア文字のイプシロン(ε)とデルタ(δ)を用いることからこのような名前になりました。
先ほどの関数でイプシロン-デルタ論法を実践すると・・・
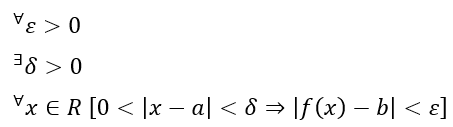
これだけ書いても数学科の人しか意味が分からないと思うので順を追って説明します。
- 一段目;任意の正の数でεを定義する (Aを逆さにした記号は「任意の」という意味)
- 二段目;ある正の数がδを定義する (ヨの記号は「ある」という意味)
- 三段目左;任意のxで0<|x-a|<δが成立する
- 三段目右;|f(x)-b|<εが成立する
上の説明をしても多くの人が「?」「これの何が極限と関係するんだ?」と思うのでさらに分かりやすく解説します。
高校の極限の問題で「近い」の程度が人によって違うことを上げました(これが鍵になります)。
ここからは、会話形式で意味を解説します。
- あなたが小さいと思う数を考えてください。それをεとします
- 続いて、私が小さいと思うある数をδとします
- 私が小さいと思うδよりも|x-a|が小さくなるxをあなたが任意に定義します
- この時、|f(x)-b」はあなたが小さいと思う値εよりも小さくなりますよね。
- だから、|x-a|<δ(x→a)の時、f(x)→bと考えて問題ないですね。
これがε-δ論法です。
「程度」の問題を克服するために、「小さい値」を自分で定義するのではなく、証明を見る人に小さいと思う数を定義させて、自分が定義したものがそれよりも小さい値だから問題ないよね、、、
という手法となっております。
実践編
イプシロン-デルタ論法を実践してみます。
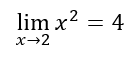
上の極限式をε-δ論法で証明します。
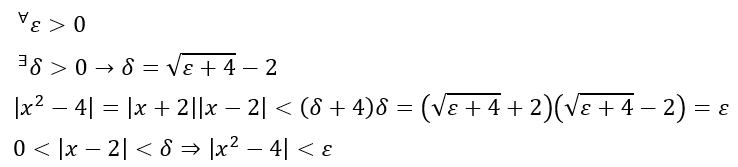
以上から極限値が4であることが分かります。
ここで、疑問として「δをεで表してるけどいいのか?」と思うかもしれませんが、εを任意で決めているということは、δをεで表したとしてもδは任意に決めれますよね?
ε-δ論法は大学受験では全く出ないです。
皆さんは高校数学の方法で極限を考えてもらっていいので安心してください。



コメント