こんにちは。Horyです。
前回の記事で、ストークスの定理を証明しました。
今回はこの定理を利用して電流と磁場の関係を紐付けたアンペールの法則(右ネジの法則)について解説します。
今回も頑張りましょう。
アンペールの法則について・・・
まず、アンペールの法則とは以下のような式が成立することです。
今回は積分系で書きます。

- 左辺・・・磁束密度の経路Cについての線積分
- 右辺・・・閉曲面を貫く電流密度の法線成分の面積分に透磁率かけた
- 電流密度・・・単位時間当たりに単位面積を通過した電荷量
電流密度(ベクトル)と電流(スカラー)の関係は以下の通りです。

電流の定義は単位面積を単位時間に通過した電荷の量を電流密度としたとき、この電流密度が断面を垂直に通過する量を面積で積分した量です。
これを当てはめて見ると・・・
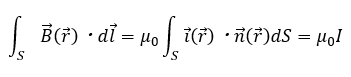
アンペールの法則は上の式を使うことは覚えておいた方が良いです。
ここで、前回証明したストークスの定理をあてはめ、アンペールの法則の微分系を作ります。
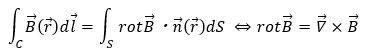
- 左辺・・・磁束密度の経路Cについての線積分
- 右辺・・・法線方向に貫く磁束密度
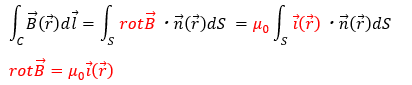
- 左辺・・・磁束密度の渦度 (rot は渦度を表している)
- 右辺・・・電流密度 (μ0は比例定数)
- 式の意味・・・磁束密度の渦度は電流密度に比例する。
上の赤い式はアンペールの法則の微分系と呼ばれている形です。
ここで、上の赤い式の部分は何でこうなってるの?と思うかもしれませんが、いったん置いておきます。これは後に出す記事で詳しく解説します。
静磁場について
電荷の流れが時間に依存しない(電流の大きさ・向きが変化しない)電流のことを定常電流といいます。
- 定常電流・・・電流の向きや大きさが変化しない
- 変位電流・・・電流の向きや大きさが時間で変化
ここで、定常電流が作る磁場のことを静磁場といいます。ここで、静電場との違いをまとめます。
- 静電場・・・止まっている電荷が作る電場
- 静磁場・・・定常電流が作る磁場(磁束密度)
ここで、重要なのは、定常電流について、磁束密度のrotが0になることです。つまり・・・
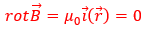
この式が成立します。何でこうなるかは別の記事で解説します。
アンペールの法則 簡単な問題
アンペールの法則を用いた簡単な問題を紹介します。

この問題を例に解説します。基本的には上で解説したことの応用です。
電流は定常電流であるとします。
アンペールの法則から、磁束密度の渦度は電流密度に比例します。だから、電流と磁束密度の関係は下図のようになっているのではないでしょうか?
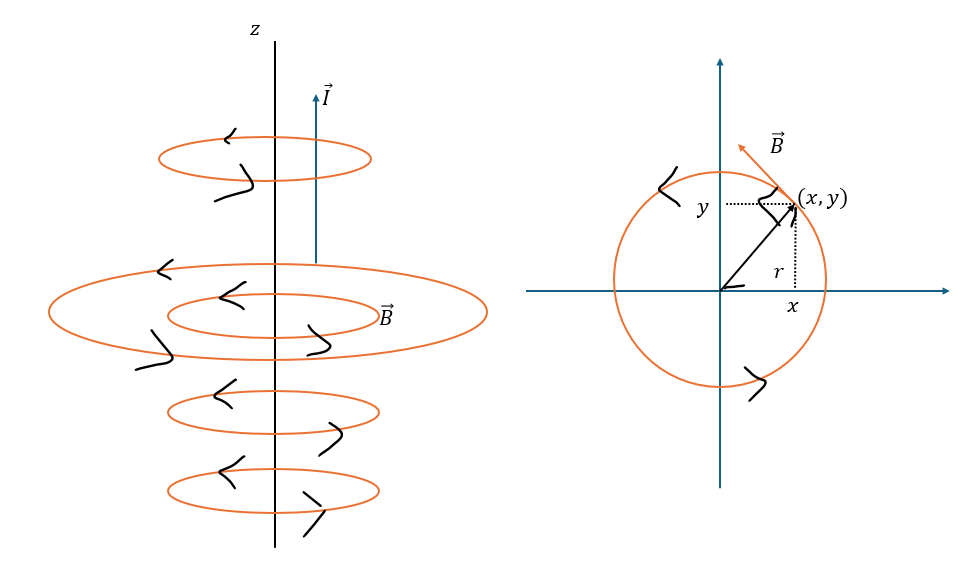
これは、一部しか書いてませんが、実際は導線の周り・上下に円状の磁束密度が無数に発生しています。
上の図の電流と磁束密度の向きを確認してください。ネジが上に進むようにするときに右に回します。だから、右ねじの法則と呼ばれています。
問題 解答・解説
アンペールの法則を用います。仮に、磁束密度の渦の半径がrの場合で考えます。
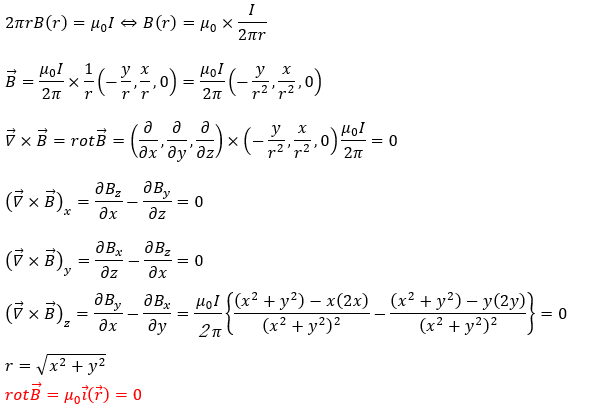
補足 微分の計算
微分の計算を行います。例えば、xで偏微分するとします。
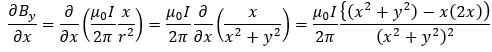
確かに、計算通りになりました。



コメント